题目内容
【题目】结果如此巧合！
下面是小颖对一道题目的解答.
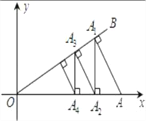
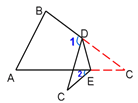
题目：如图，
的内切圆与斜边
相切于点
，
，
，求
的面积.
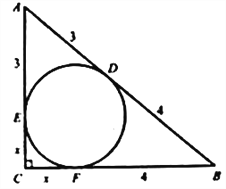
解：设的内切圆分别与
、
相切于点
、
，
的长为
.
根据切线长定理，得
，
，
.
根据勾股定理，得
.
整理，得
.
所以
.
小颖发现
恰好就是
，即的面积等于
与
的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
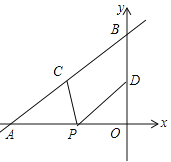
已知：的内切圆与相切于点，
，
.
可以一般化吗？
（1）若
，求证：的面积等于
.
倒过来思考呢？
（2）若
，求证.改变一下条件……
（3）若
，用
、
表示的面积.
【答案】（1）证明见解析；（2）证明见解析.（3）
.
【解析】（1）设
的内切圆分别与
、
相切于点
、
，
的长为
,仿照例题利用勾股定理得
再根据
即可得到
=mn.
（2）由
，得
, 因此
=
,利用勾股定理的逆定理可得
.
（3）过点
作
，垂足为
,在
中，
，
.所以
, 在
中根据勾股定理得
,由此
.
设的内切圆分别与、相切于点、，的长为.
根据切线长定理，得
，
，
.
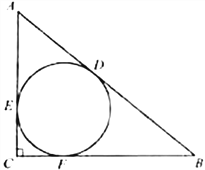
（1）如图①，在
中，根据勾股定理，得
.
整理，得.
所以
.
（2）由，得
.
整理，得.
所以
.
根据勾股定理的逆定理，得.
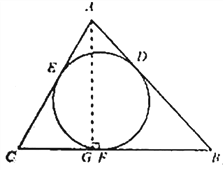
（3）如图②，过点作，垂足为.
在中，
，
.
所以
.
在中，根据勾股定理，得
.
整理，得.
所以
.
名师点拨卷系列答案
【题目】越来越多的人在用微信付款、转账，把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起，每个微信账户终身享有1000元的免费提现额度，当累计提现金额超过1000元时，累计提现金额超出1000元的部分需支付0.1%的手续费，以后每次提现支付的手续费为提现金额的0.1%.
（1）小明在今天第1次进行了提现，金额为l600元，他需支付手续费_________元；
（2）小亮自2016年3月1日至今，用自己的微信账户共提现3次，3次提现金额和手续费分别如下：
第1次 | 第2次 | 第3次 | |
提现金额（元） | A | b |
|
手续费（元） | 0 | 0.4 | 3.4 |
问：小明3次提现金额各是多少元？
（3）单笔手续费小于0.1元的，按照0.1元收取（即提现不足100元，按照100元收取手续费）.小红至今共提现两次，每次提现金额都是整数，共支付手续费2.4元，第一次提现900元。求小红第二次提现金额的范围.
