题目内容
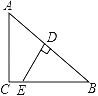
【题目】如图,在△ABC中,∠ACB=90°,AC=6,AB=10,AB的垂直平分线DE交AB于点D,交BC于点E,则CE的长等于_____.
【答案】![]()
【解析】连接AE,由垂直平分线的性质可得AE=BE,利用勾股定理可得BC=8,设CE=x,则BE=8-x,在△ACE中利用勾股定理可得x的长,即得ce的长.
解:连接AE,
∵DE为AB的垂直平分线,
∴AE=BE,
∵在△ABC中,∠ACB=90°,AC=6,AB=10,
由勾股定理得BC=8,
设CE=x,则BE=8-x,在Rt△ACE中,
由勾股定理得:x2+62=(8-x)2,
解得x=![]() ,
,
故答案为: ![]() .
.
“点睛”本题主要考查了垂直平分线的性质和勾股定理,利用方程思想是解答此题的关键.

练习册系列答案
相关题目
【题目】在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数(人) | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.1.70m,1.65mB.1.70m,1.70mC.1.65m,1.65mD.3人,4人