��Ŀ����
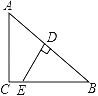
����Ŀ����������A��B��������·ME��MFλ����ͼ��ʾ������ME�Ƕ�������Ĺ�·���ֵ��Ų�������C����һ���źŷ�������Ҫ����������������A��B�ľ��������ȣ���������·ME��MF�ľ���Ҳ������ȣ�������FME���ڲ���
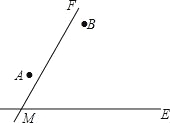
��1����CӦѡ�ںδ�������ͼ�У��ó߹���ͼ�ҳ����������ĵ�C������д��֪��������������ֻ������ͼ�ۼ���
��2����C����·ME�ľ���Ϊ2km����AB�Ĵ�ֱƽ���߽�ME�ڵ�N����M����õ�Cλ�ڵ�M�ı�ƫ��60�㷽����N��û�õ�Cλ�ڵ�N�ı�ƫ��45�㷽����MN�ij����������������
���𰸡���1����ͼ��������2��2![]() +2km
+2km
��������
�����������1��������A��B������ȵĵ����߶�AB�Ĵ�ֱƽ�����ϣ���������·������ȵĵ���������·���нǵĽ�ƽ�����ϣ��ֱ�������ֱƽ�������ƽ���ߣ����ǵĽ��㼴Ϊ�������ĵ�C��
��2����CD��MN�ڵ�D�������Ǻ����ó�MD=![]() CD��DN=CD�����ǵõ����ۣ�
CD��DN=CD�����ǵõ����ۣ�
�����������1����ͼ��ʾ����C��Ϊ����
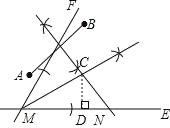
��2����CD��MN�ڵ�D��
������ã���CMN=30�㣬��CND=45�㣬
����Rt��CMD��![]() =tan��CMN��
=tan��CMN��
��MD=![]() =2
=2![]() ��
��
����Rt��CND�� ![]() =tan��CNM��
=tan��CNM��
��ND=CD=2��
��MN=DM+DN=2![]() +2km��
+2km��

 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�����Ŀ���±���ijУŮ������Ӷ�Ա������ֲ�
����/�� | 13 | 14 | 15 | 16 |
Ƶ�� | 1 | 1 | 7 | 3 |
���УŮ������Ӷ�Ա��ƽ��������( )��
A. 14.5 B. 15 C. 15.3 D. 15.5