题目内容
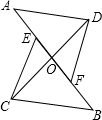已知：如图，AE=BF，AD∥BC，AD=BC，AB、CD交于O点，
求证：OE=OF．
证明：∵AD∥BC，
∴∠DAF=∠CBE，
∵AE=BF，
∴AF=BE，
又∵AD=BC，
∴△ADF≌△BCE（SAS），
∴∠AFD=∠BEC，DF=CE，
又∵∠EOC=∠FOD，
∴△EOC≌△FOD（AAS），
∴OE=OF．
分析：利用AD∥BC，先证△ADF≌△BCE，然后求证△EOC≌△FOD即可．
点评：此题求证两次全等，第一次利用（SAS）定理证明△ADF≌△BCE，第二次利用（AAS）定理证明，△EOC≌△FOD．
∴∠DAF=∠CBE，
∵AE=BF，
∴AF=BE，
又∵AD=BC，
∴△ADF≌△BCE（SAS），
∴∠AFD=∠BEC，DF=CE，
又∵∠EOC=∠FOD，
∴△EOC≌△FOD（AAS），
∴OE=OF．
分析：利用AD∥BC，先证△ADF≌△BCE，然后求证△EOC≌△FOD即可．
点评：此题求证两次全等，第一次利用（SAS）定理证明△ADF≌△BCE，第二次利用（AAS）定理证明，△EOC≌△FOD．
练习册系列答案
名校课堂系列答案
相关题目
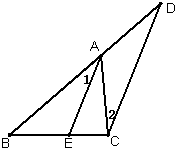26、已知，如图，AE是∠BAC的平分线，∠1=∠D．
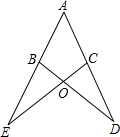已知，如图，AE=AD，BE=CD，BD、CE相交于点O，求证：∠EBD=∠DCE（要求注明理由）．
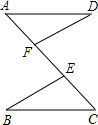已知：如图，AE=CF，∠DAF=∠BCE，AD=CB，问△ADF与△CBE全等吗？请说明理由．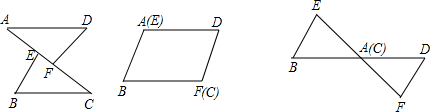
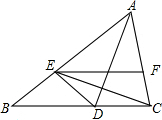已知：如图，AE=AC，EF∥BC，EC平分∠DEF．
已知：如图，AE⊥BC于E，∠1=∠2．求证：DC⊥BC．