题目内容
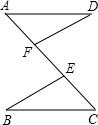 已知:如图,AE=CF,∠DAF=∠BCE,AD=CB,问△ADF与△CBE全等吗?请说明理由.
已知:如图,AE=CF,∠DAF=∠BCE,AD=CB,问△ADF与△CBE全等吗?请说明理由.如果将△BEC沿CA方向平移,可得下列三种图形.如果上述条件不变,结论仍成立吗?请说明理由.
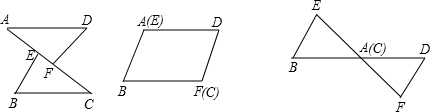
分析:(1)根据题意即可推出AF=CE,根据全等三角形的判定定理“SAS”,即可推出两三角形全等;
(2)①根据等量加等量结果仍相等的原则,即可推出AE=CF,然后根据全等三角形的判定定理“SAS”,即可推出两三角形全等,②如图,可知公共边AF,根据全等三角形的判定定理“SAS”,即可推出两三角形全等,③根据全等三角形的判定定理“SAS”,即可推出两三角形全等.
(2)①根据等量加等量结果仍相等的原则,即可推出AE=CF,然后根据全等三角形的判定定理“SAS”,即可推出两三角形全等,②如图,可知公共边AF,根据全等三角形的判定定理“SAS”,即可推出两三角形全等,③根据全等三角形的判定定理“SAS”,即可推出两三角形全等.
解答:(1)解:△ADF与△CBE全等.理由如下:
∵AE=CF,
∴AF=CE,
∵AD∥BC(已知)
∴∠DAF=∠BCE(两直线平行,内错角相等),
∴在△ADF与△CBE中,
∵
,
∴△ADF≌△CBE(SAS),
(2)解:结论仍然成立.理由如下:
①∵AF=CE,
∴AE=CF,
∴在△ADF与△CBE中,
∵
,
∴△ADF≌△CBE(SAS),
②∵在△ADF与△CBE中,
,
∴△ADF≌△CBE(SAS),
③∵在△ADF与△CBE中,
,
∴△ADF≌△CBE(SAS).
∵AE=CF,
∴AF=CE,
∵AD∥BC(已知)
∴∠DAF=∠BCE(两直线平行,内错角相等),
∴在△ADF与△CBE中,
∵
|
∴△ADF≌△CBE(SAS),
(2)解:结论仍然成立.理由如下:
①∵AF=CE,
∴AE=CF,
∴在△ADF与△CBE中,
∵
|
∴△ADF≌△CBE(SAS),
②∵在△ADF与△CBE中,
|
∴△ADF≌△CBE(SAS),
③∵在△ADF与△CBE中,
|
∴△ADF≌△CBE(SAS).
点评:本题主要考查全等三角形的判定定理、等式的性质,关键在于熟练运用判定定理“SAS”.

练习册系列答案
相关题目
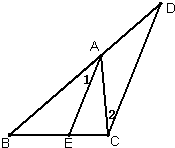 26、已知,如图,AE是∠BAC的平分线,∠1=∠D.
26、已知,如图,AE是∠BAC的平分线,∠1=∠D.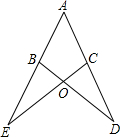 已知,如图,AE=AD,BE=CD,BD、CE相交于点O,求证:∠EBD=∠DCE(要求注明理由).
已知,如图,AE=AD,BE=CD,BD、CE相交于点O,求证:∠EBD=∠DCE(要求注明理由). 已知:如图,AE=AC,EF∥BC,EC平分∠DEF.
已知:如图,AE=AC,EF∥BC,EC平分∠DEF. 已知:如图,AE⊥BC于E,∠1=∠2.求证:DC⊥BC.
已知:如图,AE⊥BC于E,∠1=∠2.求证:DC⊥BC.