题目内容
 已知:如图,AE=AC,EF∥BC,EC平分∠DEF.
已知:如图,AE=AC,EF∥BC,EC平分∠DEF.求证:(1)ED=CD,(2)AD⊥EC.
分析:(1)根据EF∥BC可得∠1=∠3,再根据条件EC平分∠DEF,可得∠1=∠2,由等量代换可得∠2=∠3,再根据等角对等边可得ED=DC;
(2)首先证明△ACD≌△AED,根据全等三角形对应角相等可得∠4=∠5,再根据等腰三角形的三线合一的性质可得AD⊥EC.
(2)首先证明△ACD≌△AED,根据全等三角形对应角相等可得∠4=∠5,再根据等腰三角形的三线合一的性质可得AD⊥EC.
解答: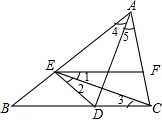 证明:(1)∵EF∥BC,
证明:(1)∵EF∥BC,
∴∠1=∠3,
∵EC平分∠DEF,
∴∠1=∠2,
∴∠2=∠3,
∴DE=DC;
(2)∵在△ACD和△AED中,
,
∴△ACD≌△AED(SSS),
∴∠4=∠5,
∴AD⊥EC.
 证明:(1)∵EF∥BC,
证明:(1)∵EF∥BC,∴∠1=∠3,
∵EC平分∠DEF,
∴∠1=∠2,
∴∠2=∠3,
∴DE=DC;
(2)∵在△ACD和△AED中,
|
∴△ACD≌△AED(SSS),
∴∠4=∠5,
∴AD⊥EC.
点评:此题主要考查了全等三角形的判定与性质,以及等腰三角形的判定与性质,关键是掌握等腰三角形底边上的中线、高线与顶角的平分线重合.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
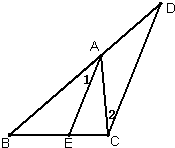 26、已知,如图,AE是∠BAC的平分线,∠1=∠D.
26、已知,如图,AE是∠BAC的平分线,∠1=∠D.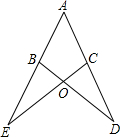 已知,如图,AE=AD,BE=CD,BD、CE相交于点O,求证:∠EBD=∠DCE(要求注明理由).
已知,如图,AE=AD,BE=CD,BD、CE相交于点O,求证:∠EBD=∠DCE(要求注明理由).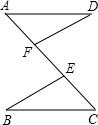 已知:如图,AE=CF,∠DAF=∠BCE,AD=CB,问△ADF与△CBE全等吗?请说明理由.
已知:如图,AE=CF,∠DAF=∠BCE,AD=CB,问△ADF与△CBE全等吗?请说明理由.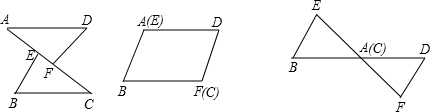
 已知:如图,AE⊥BC于E,∠1=∠2.求证:DC⊥BC.
已知:如图,AE⊥BC于E,∠1=∠2.求证:DC⊥BC.