题目内容
(2010•通州区一模)小华用两块不全等的等腰直角三角形的三角板摆放图形.(1)如图①所示△ABC,△DBE,两直角边交于点F,过点F作FG∥BC交AB于点G,连接BF、AD,则线段BF与线段AD的数量关系是______;直线BF与直线AD的位置关系是______,并求证:FG+DC=AC;
(2)如果小华将两块三角板△ABC,△DBE如图②所示摆放,使D、B、C三点在一条直线上,AC、DE的延长线相交于点F,过点F作FG∥BC,交直线AE于点G,连接AD,FB,则FG、DC、AC之间满足的数量关系式是______;
(3)在(2)的条件下,若AG=
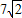 ,DC=5,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段FG于P、Q两点(如图③),线段DF分别与线段BQ、BP相交于M、N两点,若PG=2,求线段MN的长.
,DC=5,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段FG于P、Q两点(如图③),线段DF分别与线段BQ、BP相交于M、N两点,若PG=2,求线段MN的长.
【答案】分析:(1)BF、ED的数量关系应该是相等,可通过证△BEF≌△BEA来得到这个结论,易证得△AEF、△BED都是等腰直角三角形,则AE=EF、BE=DE,即可证得所求的三角形全等;进而可得∠BFE=∠BAD,由于∠EBF、∠BFE互余,因此∠EBF、∠BAD也互余,由此得BF、AD互相垂直;易知△AFG、△CDF是等腰直角三角形,则AF=FG、CD=CF,即可证得AC=FG+CD.
(2)解法同(1).
(3)此题较复杂,易得△ABC、△FCD、△AFG、△BED都是等腰直角三角形,根据已知条件先求得AC、BC、BD、CF、BG的长,过B作BH⊥FG于H,过P作PK⊥AG于K;已知PG的长,易求得PK、KG的值,进而可求得BK的长;易证得△BQH∽△BPK,根据得到的比例线段,可求得QH的长,进而可得FQ的长,然后通过△FQM∽△DBM,可求得DM的长,进而由△BDN∽△PFN求出DN的值,即可根据MN=DM-DN求出MN的值.
解答:解:(1)结论:
则线段BF与线段AC的数量关系是:相等;直线BF与直线AC的位置关系是:互相垂直;(1分)
理由:∵△ABD是等腰直角三角形,且FG∥BD,
∴△AFG、△AEF都是等腰直角三角形;
而∠ABD=∠FCD=45°,则△BEC也是等腰直角三角形,
∴AE=EF,BE=CF,
又∵∠AEC=∠BEF=90°,
∴△BEF≌△CEA,得BF=AC,∠BFE=∠CAE;
∵∠EBF+∠BFE=90°,故∠EBF+∠CAE=90°,即BF、AC互相垂直.
证明:∵△ABC、△BDE是等腰直角三角形
∴∠ABC=∠BAC=∠BDE=45°,
∵AD⊥BC,
∴∠CFD=45°,
∴CD=CF;(2分)
∵FG∥BC,∠AGF=∠ABC=45°,
∴FG=AF,
∵AD=AF+FC,
∴AD=FG+DC.(3分)
(2)FG、DC、AD之间满足的数量关系式是FG=DC+AC(解法同(1)).(4分)
(3)过点B作BH⊥FG垂足为H,过点P作PK⊥AG垂足为K;(5分)
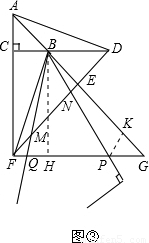 ∵FG∥BC,C、D、B在一条直线上,
∵FG∥BC,C、D、B在一条直线上,
可证△AFG、△DCF是等腰直角三角形,
∵AG=7 ,CD=5,
,CD=5,
∴根据勾股定理得:AF=FG=7,FD=5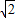 ,
,
∴AC=BC=2,
∴BD=3;
∵BH⊥FG,
∴BH∥CF,∠BHF=90°,
∵FG∥BC,
∴四边形CFHB是矩形,
∴BH=5,FH=2;
∵FG∥BC,
∴∠G=45°,
∴HG=BH=5,BG=5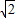 ;
;
∵PK⊥AG,PG=2,
∴PK=KG=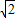 ,
,
∴BK=5 -
-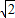 =4
=4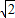 ;
;
∵∠PBQ=45°,∠HGB=45°,
∴∠GBH=45°,
∴∠1=∠2;
∵PK⊥AG,BH⊥FG,
∴∠BHQ=∠BKP=90°,
∴△BQH∽△BPK,
∴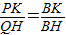 ,
,
∴QH= ,(6分)
,(6分)
∴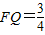 ;
;
∵FG∥BC,
∴∠D=∠MFQ,∠CBM=∠FQM,
∴△FQM∽△DBM,可求得DM=4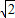 ;(7分)
;(7分)
∵∠D=∠MFQ,∠DNB=∠FNP,
∴△BDN∽△PFN,
∴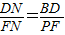 ,
,
∴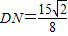 ,
,
∴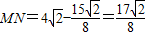 .(8分)
.(8分)
点评:此题考查了等腰直角三角形的性质、全等三角形及相似三角形的判定和性质等知识的综合应用,难度较大.
(2)解法同(1).
(3)此题较复杂,易得△ABC、△FCD、△AFG、△BED都是等腰直角三角形,根据已知条件先求得AC、BC、BD、CF、BG的长,过B作BH⊥FG于H,过P作PK⊥AG于K;已知PG的长,易求得PK、KG的值,进而可求得BK的长;易证得△BQH∽△BPK,根据得到的比例线段,可求得QH的长,进而可得FQ的长,然后通过△FQM∽△DBM,可求得DM的长,进而由△BDN∽△PFN求出DN的值,即可根据MN=DM-DN求出MN的值.
解答:解:(1)结论:
则线段BF与线段AC的数量关系是:相等;直线BF与直线AC的位置关系是:互相垂直;(1分)
理由:∵△ABD是等腰直角三角形,且FG∥BD,
∴△AFG、△AEF都是等腰直角三角形;
而∠ABD=∠FCD=45°,则△BEC也是等腰直角三角形,
∴AE=EF,BE=CF,
又∵∠AEC=∠BEF=90°,
∴△BEF≌△CEA,得BF=AC,∠BFE=∠CAE;
∵∠EBF+∠BFE=90°,故∠EBF+∠CAE=90°,即BF、AC互相垂直.
证明:∵△ABC、△BDE是等腰直角三角形
∴∠ABC=∠BAC=∠BDE=45°,
∵AD⊥BC,
∴∠CFD=45°,
∴CD=CF;(2分)
∵FG∥BC,∠AGF=∠ABC=45°,
∴FG=AF,
∵AD=AF+FC,
∴AD=FG+DC.(3分)
(2)FG、DC、AD之间满足的数量关系式是FG=DC+AC(解法同(1)).(4分)
(3)过点B作BH⊥FG垂足为H,过点P作PK⊥AG垂足为K;(5分)
 ∵FG∥BC,C、D、B在一条直线上,
∵FG∥BC,C、D、B在一条直线上,可证△AFG、△DCF是等腰直角三角形,
∵AG=7
 ,CD=5,
,CD=5,∴根据勾股定理得:AF=FG=7,FD=5
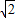 ,
,∴AC=BC=2,
∴BD=3;
∵BH⊥FG,
∴BH∥CF,∠BHF=90°,
∵FG∥BC,
∴四边形CFHB是矩形,
∴BH=5,FH=2;
∵FG∥BC,
∴∠G=45°,
∴HG=BH=5,BG=5
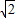 ;
;∵PK⊥AG,PG=2,
∴PK=KG=
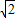 ,
,∴BK=5
 -
-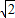 =4
=4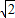 ;
;∵∠PBQ=45°,∠HGB=45°,
∴∠GBH=45°,
∴∠1=∠2;
∵PK⊥AG,BH⊥FG,
∴∠BHQ=∠BKP=90°,
∴△BQH∽△BPK,
∴
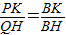 ,
,∴QH=
 ,(6分)
,(6分)∴
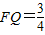 ;
;∵FG∥BC,
∴∠D=∠MFQ,∠CBM=∠FQM,
∴△FQM∽△DBM,可求得DM=4
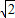 ;(7分)
;(7分)∵∠D=∠MFQ,∠DNB=∠FNP,
∴△BDN∽△PFN,
∴
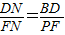 ,
,∴
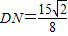 ,
,∴
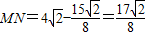 .(8分)
.(8分)点评:此题考查了等腰直角三角形的性质、全等三角形及相似三角形的判定和性质等知识的综合应用,难度较大.

练习册系列答案
相关题目
 .
.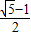 AB.
AB.
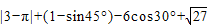 .
.