题目内容
(2010•通州区一模)已知:如图,在△ABC中,AB=AC,∠ABC=36°,将△ABC绕着点B逆时针旋转36°后得到△EBF,点A落在点E处,点C落在点F处,连接CF.请你画出图形,并按下面要求完成本题.(1)求证四边形BCFE是等腰梯形;
(2)求证:AF=
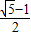 AB.
AB.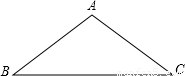
【答案】分析:(1)由于旋转得到的图形中点B、A、F在一条直线上,∠ABC=∠EFB=36°,又EB=BA,CA=CF,则BE=CF,四边形BCFE是等腰梯形即可得证.
(2)由(1)证明知△CFA∽△BCF,则 ,变形得
,变形得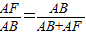 ,则即可证得AF=
,则即可证得AF=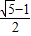 AB.
AB.
解答: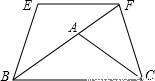 证明:所作图形如下:
证明:所作图形如下:
(1)∵△BEF由△ABC绕着点B逆时针旋转36°得到,且∠ABC=36°.
∴点B、A、F在一条直线上,且BF=BC,AB=AC=BE=EF,
∠ABC=∠EBF=∠ACB=∠EFB=36°.
∴EF∥BC.
∵BF=BC,∠ABC=∠ACB=36°,
∴∠BFC=∠FCB=72°,∠BAC=108°.
∴∠FAC=72°.
∴AC=CF.
∴BE=CF.
∴四边形EBCF是等腰梯形.
(2)由(1)证明知△CFA∽△BCF,
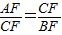 ,
,
即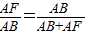 .
.
解之: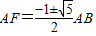 .
.
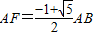 .
.
点评:本题考查了相似三角形的判定与性质及等腰梯形的判定问题,要求学生能够熟练掌握合并应用.
(2)由(1)证明知△CFA∽△BCF,则
 ,变形得
,变形得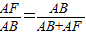 ,则即可证得AF=
,则即可证得AF=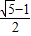 AB.
AB.解答:
 证明:所作图形如下:
证明:所作图形如下:(1)∵△BEF由△ABC绕着点B逆时针旋转36°得到,且∠ABC=36°.
∴点B、A、F在一条直线上,且BF=BC,AB=AC=BE=EF,
∠ABC=∠EBF=∠ACB=∠EFB=36°.
∴EF∥BC.
∵BF=BC,∠ABC=∠ACB=36°,
∴∠BFC=∠FCB=72°,∠BAC=108°.
∴∠FAC=72°.
∴AC=CF.
∴BE=CF.
∴四边形EBCF是等腰梯形.
(2)由(1)证明知△CFA∽△BCF,
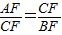 ,
,即
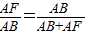 .
.解之:
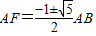 .
.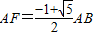 .
.点评:本题考查了相似三角形的判定与性质及等腰梯形的判定问题,要求学生能够熟练掌握合并应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 .
.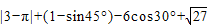 .
.