题目内容
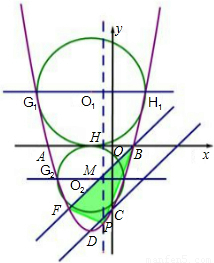
(2010•通州区一模)在平面直角坐标系中,抛物线y=x2+2x-3与x轴交于A、B两点,(点A在点B左侧).与y轴交于点C,顶点为D,直线CD与x轴交于点E.(1)请你画出此抛物线,并求A、B、C、D四点的坐标;
(2)将直线CD向左平移两个单位,与抛物线交于点F(不与A、B两点重合),请你求出F点坐标;
(3)在点B、点F之间的抛物线上有一点P,使△PBF的面积最大,求此时P点坐标及△PBF的最大面积;
(4)若平行于x轴的直线与抛物线交于G、H两点,以GH为直径的圆与x轴相切,求该圆半径.
【答案】分析:(1)抛物线的解析式中,令x=0,可求得点C的坐标,令y=0,可求得A、B的坐标;利用配方法将抛物线的解析式化为顶点坐标式,即可求得顶点D的坐标.
(2)易求得直线CD的解析式,利用左加右减的平移规律,可得到平移后的直线解析式,联立抛物线的解析式,即可求得点F的坐标.
(3)过P作PM∥y轴交直线BF(题2平移后的直线)于M,设出点P的横坐标,根据抛物线和直线的解析式,可求得P、M的纵坐标,从而得到PM的长,以PM为底、B、F的横坐标差的绝对值为高,即可求得△BFP的面积表达式(也可由△BMP、△FMP的面积和求得),也就得到了关于△BFP的面积和P点横坐标的函数关系式,根据函数的性质即可求出△BFP的最大面积及对应的P点坐标.(也可先求得PM的最大值,然后再求出此时△BFP的最大面积)
(4)若易G、H的圆与x轴相切,那么G、H纵坐标的绝对值等于圆的半径,且圆心在抛物线的对称轴上,可用圆的半径分别表示出G、H的坐标,将它们代入抛物线的解析式中,即可求得该圆的半径.(需要注意的是,在表示G、H的坐标时,要分圆心在x轴上、下方两种情况讨论.)
解答:解:(1)抛物线y=x2+2x-3中,x=0,则y=-3;y=0,则x=1或-3;
∴A(-3,0),B(1,0),C(0,-3);
∵y=x2+2x-3=(x+1)2-4,
∴D(-1,-4);
故A(-3,0),B(1,0),C(0,-3),D(-1,-4).(2分)
(2)∵C(0,-3),D(-1,-4),
∴直线CD:y=x-3;
将直线CD向左平移两个单位,得:
y=(x+2)-3=x-1,
此时直线经过点B(1,0);
联立抛物线的解析式有:
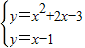 ,
,
解得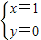 ,
,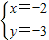 ;
;
∴F(-2,-3).(3分)
(3)过点P作y轴的平行线与BF交于点M,与x轴交于点H.
易得F(-2,-3),直线BF解析式为y=x-1.
设P(x,x2+2x-3),则M(x,x-1),(4分)
∴PM=-x2-x+2=-(x+ )2+
)2+ ;
;
PM的最大值是 ,此时x=-
,此时x=- ,
,
当PM取最大值时△PBF的面积最大,
S△PBF=S△PFM+S△PEM=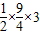 ,
,
△PFB的面积的最大值为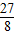 ,P点坐标为:(-
,P点坐标为:(- ,-
,-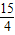 ).
).
(4)如图,①当直线GH在x轴上方时,设圆的半径为R(R>0),则H(R-1,R),
代入抛物线的表达式,
解得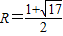 ;(7分)
;(7分)
②当直线GH在x轴下方时,设圆的半径为r(r>0),
则H(r-1,-r),
代入抛物线的表达式,
解得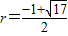
∴圆的半径为 或
或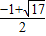 .(8分)
.(8分)
点评:此题考查了二次函数图象与坐标轴交点坐标的求法、函数图象的平移、图象交点坐标的求法、图形面积的求法、切线的性质等重要知识点.要注意的是(4)题中,应该考虑到在x轴的上、下方都存在符合条件的圆,一定要分类讨论,以免漏解.
(2)易求得直线CD的解析式,利用左加右减的平移规律,可得到平移后的直线解析式,联立抛物线的解析式,即可求得点F的坐标.
(3)过P作PM∥y轴交直线BF(题2平移后的直线)于M,设出点P的横坐标,根据抛物线和直线的解析式,可求得P、M的纵坐标,从而得到PM的长,以PM为底、B、F的横坐标差的绝对值为高,即可求得△BFP的面积表达式(也可由△BMP、△FMP的面积和求得),也就得到了关于△BFP的面积和P点横坐标的函数关系式,根据函数的性质即可求出△BFP的最大面积及对应的P点坐标.(也可先求得PM的最大值,然后再求出此时△BFP的最大面积)
(4)若易G、H的圆与x轴相切,那么G、H纵坐标的绝对值等于圆的半径,且圆心在抛物线的对称轴上,可用圆的半径分别表示出G、H的坐标,将它们代入抛物线的解析式中,即可求得该圆的半径.(需要注意的是,在表示G、H的坐标时,要分圆心在x轴上、下方两种情况讨论.)
解答:解:(1)抛物线y=x2+2x-3中,x=0,则y=-3;y=0,则x=1或-3;
∴A(-3,0),B(1,0),C(0,-3);
∵y=x2+2x-3=(x+1)2-4,
∴D(-1,-4);
故A(-3,0),B(1,0),C(0,-3),D(-1,-4).(2分)
(2)∵C(0,-3),D(-1,-4),
∴直线CD:y=x-3;
将直线CD向左平移两个单位,得:
y=(x+2)-3=x-1,
此时直线经过点B(1,0);
联立抛物线的解析式有:
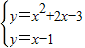 ,
,解得
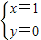 ,
,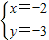 ;
;∴F(-2,-3).(3分)
(3)过点P作y轴的平行线与BF交于点M,与x轴交于点H.
易得F(-2,-3),直线BF解析式为y=x-1.
设P(x,x2+2x-3),则M(x,x-1),(4分)
∴PM=-x2-x+2=-(x+
 )2+
)2+ ;
;
PM的最大值是
 ,此时x=-
,此时x=- ,
,当PM取最大值时△PBF的面积最大,
S△PBF=S△PFM+S△PEM=
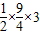 ,
,△PFB的面积的最大值为
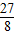 ,P点坐标为:(-
,P点坐标为:(- ,-
,-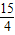 ).
).(4)如图,①当直线GH在x轴上方时,设圆的半径为R(R>0),则H(R-1,R),
代入抛物线的表达式,
解得
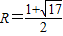 ;(7分)
;(7分)②当直线GH在x轴下方时,设圆的半径为r(r>0),
则H(r-1,-r),
代入抛物线的表达式,
解得
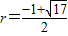
∴圆的半径为
 或
或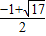 .(8分)
.(8分)点评:此题考查了二次函数图象与坐标轴交点坐标的求法、函数图象的平移、图象交点坐标的求法、图形面积的求法、切线的性质等重要知识点.要注意的是(4)题中,应该考虑到在x轴的上、下方都存在符合条件的圆,一定要分类讨论,以免漏解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. AB.
AB.
 .
.