Question

（2013•滨湖区二模）如图，已知点A是双曲线y=

3

x

在第一象限上的一动点，连接AO，以OA为一边作等腰直角三角形AOB（∠AOB=90°），点B在第四象限，随着点A的运动，点B的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为

y=-

3

x

．

Answer 1

分析：设点B所在反比例函数的解析式为y=

k

x

（k≠0），分别过点AB作AD⊥x轴于点D，BE⊥x轴于点E，由全等三角形的判定定理可知Rt△AOD≌Rt△OBE，故可得出OE•BE=-AD•OD，再根据点A在双曲线y=

3

x

上即可得出结论．

解答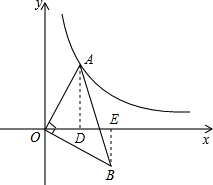：解：设点B所在反比例函数的解析式为y=

k

x

（k≠0），分别过点AB作AD⊥x轴于点D，BE⊥x轴于点E，
∵∠AOE+∠DOB=90°，∠AOE+∠OAD=90°，
∴∠OAD=∠BOE，
同理可得∠AOD=∠OBE，
∵在Rt△AOD与Rt△OBE中，

∠OAD=∠BOE OA=OB ∠AOD=∠OBE

，
∴Rt△AOD≌Rt△OBE（ASA），
∵点B在第二象限，
∴OE•BE=-AD•OD，即k=-3，
∴反比例函数的解析式为：y=-

3

x

．
故答案为：y=-

3

x

．

点评：本题考查的是反比例函数综合题，熟知反比例函数y=

k

x

（k≠0）中，k=xy为定值是解答此题的关键．