题目内容
（2012•永州）如图，已知圆O的半径为4，∠A=45°，若一个圆锥的侧面展开图与扇形OBC能完全重合，则该圆锥的底面圆的半径为1
1
．分析：首先求得扇形的圆心角BOC的度数，然后求得扇形的弧长，利用弧长等于圆的底面周长求得圆锥的底面圆的半径即可．
解答：解：∵∠A=45°，
∴∠BOC=90°
∴扇形BOC的弧长为
=2π，
设圆锥的底面半径为r，则2πr=2π
解得r=1，
故答案为1．
∴∠BOC=90°
∴扇形BOC的弧长为
| 90π×4 |
| 180 |
设圆锥的底面半径为r，则2πr=2π
解得r=1，
故答案为1．
点评：本题考查了圆锥的计算，解题的关键是正确的进行圆锥的有关元素和扇形的有关元素之间的转化．
练习册系列答案
相关题目
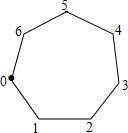（2012•永州）如图，一枚棋子放在七角棋盘的第0号角，现依逆时针方向移动这枚棋子，其各步依次移动1，2，3，…，n个角，如第一步从0号角移动到第1号角，第二步从第1号角移动到第3号角，第三步从第3号角移动到第6号角，…．若这枚棋子不停地移动下去，则这枚棋子永远不能到达的角的个数是（ ）
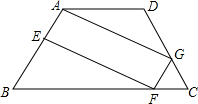（2012•永州）如图，在等腰梯形ABCD中，AD∥BC，点E、F、G分别在边AB、BC、CD上，且AE=GF=GC．求证：四边形AEFG为平行四边形．
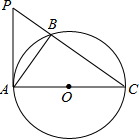（2012•永州）如图，AC是⊙O的直径，PA是⊙O的切线，A为切点，连接PC交⊙O于点B，连接AB，且PC=10，PA=6．
过点（0，-2）且与x轴平行的直线，P（m，n）是该二次函数图象上的任意一点，过P作PH⊥l，H为垂足．