题目内容
【题目】如图,以△ABC的边AB、AC为腰分别向外作等腰直角三角形ABD和等腰直角三角形ACE,连接DE.若M为BC中点,MA延长线交DE于点H,
(1) 求证:AH⊥DE.
(2) 若DE=4,AH=3,求△ABM的面积

【答案】(1)见解析;(2)3
【解析】
(1)延长AM至点F,使MF=AM,连接BF,直接证明△AMC≌△FMB,然后通过角度转换得到∠FBA=∠DAE,再证明FBA≌△EAD,即可求得∠AHE=90°;(2)DE=4,AH=3,求出S△ADE,从而得出S△ABC,M为BC的中点,即可求得△ABM的面积.
(1)延长AM至点F,使MF=AM,连接BF,
∵M为BC的中点,∠AMC=∠BMF,
在△AMC和△FMB中
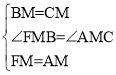
∴△AMC≌△FMB(SAS)
∴∠BFM=∠MAC,∠FBM=∠MCA,BF=CA,
△ABD和△ACE都为等腰直角三角形,
∴∠DAE=180°-∠BAC,
∴∠FBA=∠DAE,
在△FBA和△EAD中

∴△FBA≌△EAD(SAS),
∴∠BFA=∠AED,
∵∠EAC=90°,
∴∠MAC+∠HAE=90°,
∴∠HAE+∠DEA=90°,
∴∠AHE=90°,
∴AH⊥DE;
(2)∵DE=4,AH=3,
∴S△ADE=3×4÷2=6,
∴S△FBA=6,即S△ABC=6,
∵M为BC的中点,
∴S△ABM=3


练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目




