题目内容
【题目】 已知△ABC中，∠A=25°，∠B=40°． 
（1）求作：⊙O，使得⊙O经过A、C两点，且圆心O落在AB边上．（要求尺规作图，保留作图痕迹，不必写作法）
（2）求证：BC是（1）中所作⊙O的切线．
【答案】
（1）解：作图如图1：
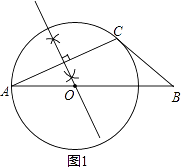
（2）证明：如图2，
连接OC，
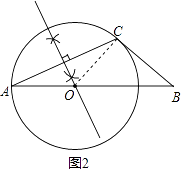
∵OA=OC，∠A=25°
∴∠BOC=50°，
又∵∠B=40°，
∴∠BOC+∠B=90°
∴∠OCB=90°
∴OC⊥BC
∴BC是⊙O的切线．
【解析】（1）作出线段AC的垂直平分线进而得出AC垂直平分线与线段AB的交点O，进而以AO为半径做圆即可；（2）连接CO，再利用已知得出∠OCB=90°，进而求出即可．
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识，掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
