��Ŀ����
��2013•������һģ����ͼ������ԭ���������y=-x2+2mx��x�����һ������ΪA����P��һ�κ���y=2x-2m��ͼ���ϣ�PH��x����H��ֱ��AP��y���ڵ�C����P�ĺ�����Ϊ1������C�����O�غϣ�
��1����ͼ1����m=-1ʱ�����P�����꣮
��2����ͼ2����0��m��
ʱ����mΪ��ֵʱ
=2��
��3���Ƿ����m��ʹ
=2�������ڣ������������Ҫ���m��ֵ�����������Ӧ�ĵ�P���ꣻ�������ڣ���˵�����ɣ�
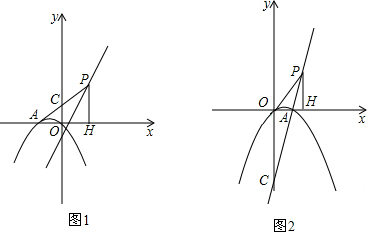
��1����ͼ1����m=-1ʱ�����P�����꣮
��2����ͼ2����0��m��
| 1 |
| 2 |
| CP |
| AP |
��3���Ƿ����m��ʹ
| CP |
| AP |

��������1���Ƚ�m=-1����y=2x-2m���õ�y=2x+2������x=1�����y=4�����������P�����ꣻ
��2������PH��OC���ó���PAH�ס�CAO���������������ζ�Ӧ�߳ɱ����õ�
=
����
=2���ó�OA=
���ٽⷽ��-x2+2mx=0�������A�����꣨2m��0������2m=
��m=
��
��3��������������ۣ��ٵ�0��m��
ʱ���ɣ�2����m=
����m=
����y=2x-2m���õ�y=2x-
���ٽ�x=1���룬���y��ֵ���õ���P�����ꣻ
�ڵ�
��m��1ʱ������PH��OC���ó���APH�ס�ACO���������������ζ�Ӧ�߳ɱ����õ�
=
����
=2���ó�OA=
���ⷽ��2m=
���ó�m=
����ͬ�٣�
�۵�m��1ʱ��ͬ�ڣ����m=
��ȥ��
�ܵ�m��0ʱ������PH��OC���ó���APH�ס�ACO���������������ζ�Ӧ�߳ɱ����õ�
=
����
=2���ó�CP��AP����CP��AP������m��ֵ�����ڣ�
��2������PH��OC���ó���PAH�ס�CAO���������������ζ�Ӧ�߳ɱ����õ�
| PA |
| CA |
| AH |
| AO |
| CP |
| AP |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
��3��������������ۣ��ٵ�0��m��
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
�ڵ�
| 1 |
| 2 |
| PA |
| CA |
| AH |
| AO |
| CP |
| AP |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
�۵�m��1ʱ��ͬ�ڣ����m=
| 3 |
| 4 |
�ܵ�m��0ʱ������PH��OC���ó���APH�ס�ACO���������������ζ�Ӧ�߳ɱ����õ�
| PA |
| CA |
| AH |
| AO |
| CP |
| AP |
��� �⣺��1����ͼ1����m=-1ʱ��y=2x+2��
�⣺��1����ͼ1����m=-1ʱ��y=2x+2��
��x=1����y=4��
���P��������1��4����
��2����ͼ2����PH��x�ᣬ��PH��OC��
���PAH�ס�CAO����
=
��
��
=2����
=
=1����OA=
��
��y=0����-x2+2mx=0��
��x1=0��x2=2m��
���A�����꣨2m��0����
��2m=
����m=
��
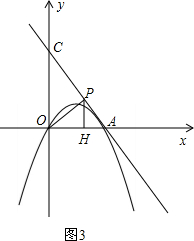
��3���ٵ�0��m��
ʱ���ɣ�2����m=
��
��y=2x-
��
��x=1����y=
��
���P��������1��
����
����ͼ3����
��m��1ʱ��
��PH��x�ᣬ��PH��OC��
���APH�ס�ACO����
=
��
��
=2����
=
����OH=
OA��
��OH=1����OA=
��
 ��2m=
��2m=
��m=
��
��y=2x-
��
��x=1����y=
��
���P��������1��
����
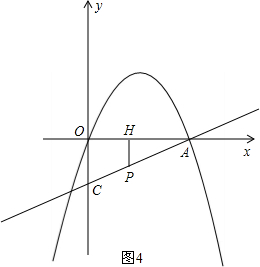
����ͼ4����m��1ʱ��
��PH��x�ᣬ��PH��OC��
���APH�ס�ACO����
=
��
��
=2����
=
����OH=
OA��
��OH=1����OA=
��
��2m=
��m=
��
 ��m��1����m=
��m��1����m=
��ȥ��
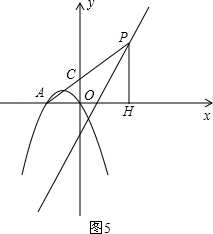
����ͼ5����m��0ʱ��
��PH��x�ᣬ��PH��OC��
���APH�ס�ACO����
=
��
��
=2����CP��AP��
�֡�CP��AP��
��m��ֵ�����ڣ�
 �⣺��1����ͼ1����m=-1ʱ��y=2x+2��
�⣺��1����ͼ1����m=-1ʱ��y=2x+2����x=1����y=4��
���P��������1��4����
��2����ͼ2����PH��x�ᣬ��PH��OC��
���PAH�ס�CAO����
| PA |
| CA |
| AH |
| AO |
��
| CP |
| AP |
| PA |
| CA |
| AH |
| AO |
| 1 |
| 2 |
��y=0����-x2+2mx=0��
��x1=0��x2=2m��
���A�����꣨2m��0����
��2m=
| 1 |
| 2 |
| 1 |
| 4 |

��3���ٵ�0��m��
| 1 |
| 2 |
| 1 |
| 4 |
��y=2x-
| 1 |
| 2 |
��x=1����y=
| 3 |
| 2 |
���P��������1��
| 3 |
| 2 |
����ͼ3����
| 1 |
| 2 |
��PH��x�ᣬ��PH��OC��
���APH�ס�ACO����
| PA |
| CA |
| AH |
| AO |
��
| CP |
| AP |
| AH |
| AO |
| 1 |
| 3 |
| 2 |
| 3 |
��OH=1����OA=
| 3 |
| 2 |
 ��2m=
��2m=| 3 |
| 2 |
| 3 |
| 4 |
��y=2x-
| 3 |
| 2 |
��x=1����y=
| 1 |
| 2 |
���P��������1��
| 1 |
| 2 |
����ͼ4����m��1ʱ��
��PH��x�ᣬ��PH��OC��
���APH�ס�ACO����
| PA |
| CA |
| AH |
| AO |
��
| CP |
| AP |
| AH |
| AO |
| 1 |
| 3 |
| 2 |
| 3 |
��OH=1����OA=
| 3 |
| 2 |
��2m=
| 3 |
| 2 |
| 3 |
| 4 |
 ��m��1����m=
��m��1����m=| 3 |
| 4 |
����ͼ5����m��0ʱ��
��PH��x�ᣬ��PH��OC��
���APH�ס�ACO����
| PA |
| CA |
| AH |
| AO |
��
| CP |
| AP |
�֡�CP��AP��
��m��ֵ�����ڣ�
�����������Ƕ��κ������ۺ����ͣ������漰����֪ʶ���к���ͼ���ϵ���������������κ�����һԪ���η��̵Ĺ�ϵ�����������ε��ж������ʣ��Ѷ����У��ڣ�3��С�������÷�������˼�뽫m��ȡֵ���ַ�Χ���һ�����Ӧͼ�Σ��Ӷ��������ν�ϼ�����˼���������DZ�С��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��2013•������һģ����ͼ����֪AB��CD��ֱ��EF�ֱ�AB��CD�ڵ� E��F��FGƽ�֡�EFD��AB�ڵ�G������EFD=70�㣬���EGF�Ķ����ǣ�������
��2013•������һģ����ͼ����֪AB��CD��ֱ��EF�ֱ�AB��CD�ڵ� E��F��FGƽ�֡�EFD��AB�ڵ�G������EFD=70�㣬���EGF�Ķ����ǣ������� ��2013•������һģ����ͼ����DEF���ɡ�ABCͨ��ƽ�Ƶõ����ҵ�B��E��C��F��ͬһ��ֱ���ϣ���BF=14��EC=6����BE�ij����ǣ�������
��2013•������һģ����ͼ����DEF���ɡ�ABCͨ��ƽ�Ƶõ����ҵ�B��E��C��F��ͬһ��ֱ���ϣ���BF=14��EC=6����BE�ij����ǣ������� ��2013•������һģ�����κ���
��2013•������һģ�����κ���