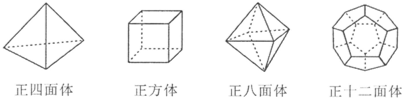
��Ŀ����
35���������ᣬ��������ֵ�ʱ�᳡�ϣ�����������ͷ�Сװ�Σ������и��ָ���������ͼ�Σ�

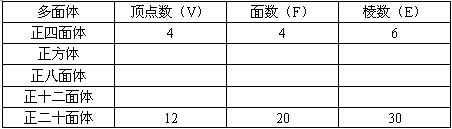
��1����һ��ÿһ����������еĶ�������V����������E����������F�������Ұѽ���������
��2���۲�������ݣ����������Ķ�������V����������E����������F��֮��Ĺ�ϵ��
��3��ΰ�����ѧ��ŷ����Euler 1707-1783��֤������һ���˾�̾�Ĺ�ϵʽ����ŷ����ʽ������֪һ��������Ķ�����V=196���������E=294��������ŷ����ʽ������������������

��1����һ��ÿһ����������еĶ�������V����������E����������F�������Ұѽ���������
| ������ | ��������V�� | ������F�� | ������E�� |
| �������� | 4 | 4 | 6 |
| ������ | |||
| �������� | |||
| ��ʮ������ | |||
| ����ʮ���� | 12 | 20 | 30 |
��3��ΰ�����ѧ��ŷ����Euler 1707-1783��֤������һ���˾�̾�Ĺ�ϵʽ����ŷ����ʽ������֪һ��������Ķ�����V=196���������E=294��������ŷ����ʽ������������������
��������1������ͼ��������������������������������ɣ�
��2�����ݱ������ݣ��������������ĺͼ�ȥ��������2���н��
��3���Ѷ���������������ŷ����ʽ���м��㼴����⣮
��2�����ݱ������ݣ��������������ĺͼ�ȥ��������2���н��
��3���Ѷ���������������ŷ����ʽ���м��㼴����⣮
����⣺��1�������ʾ��
��2����4+4-6=2��
8+6-12=2��
6+8-12=2��
20+12-30=2��
12+20-30=2��
��V+F-E=2��
��3����V+F-E=2��
����196+F-294=2��
F=294+2-196=100��
����һ��100���壮
| ������ | 8 | 6 | 12 |
| �������� | 6 | 8 | 12 |
| ��ʮ������ | 20 | 12 | 30 |
8+6-12=2��
6+8-12=2��
20+12-30=2��
12+20-30=2��
��V+F-E=2��
��3����V+F-E=2��
����196+F-294=2��
F=294+2-196=100��
����һ��100���壮
�����������Ƕ�ŷ����ʽ�Ŀ��飬�۲�ͼ��ȷ������ͼ�εĶ������������������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
�������ᣬ��������ֵ�ʱ�᳡�ϣ�����������ͷ�Сװ�Σ������и��ָ���������ͼ�Σ�

��1����һ��ÿһ����������еĶ�������V����������E����������F�������Ұѽ���������
| ������ | ��������V�� | ������F�� | ������E�� |
| �������� | 4 | 4 | 6 |
| ������ | |||
| �������� | |||
| ��ʮ������ | |||
| ����ʮ���� | 12 | 20 | 30 |
��3��ΰ�����ѧ��ŷ����Euler 1707-1783��֤������һ���˾�̾�Ĺ�ϵʽ����ŷ����ʽ������֪һ��������Ķ�����V=196���������E=294��������ŷ����ʽ������������������
����������������ֵ�ʱ�᳡�ϣ�����������ͷ�Сװ��Ʒ�������и��ָ���������ͼ�Σ�
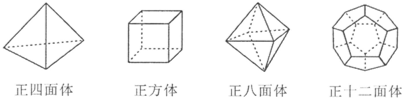
������һ������ͼ��ÿһ������ͼ�ξ��еĶ�������v����������e����������f����������������±��У�
| ���� | ������״ | ��������v�� | ������e�� | ������f�� |
| �������� | �������� | |||
| ������ | ������ | |||
| �������� | �������� | |||
| ��ʮ������ | ������� |