题目内容
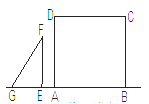
【题目】如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90° 
(1)求证:CE=BD;
(2)求证:CE⊥BD.
【答案】
(1)证明:∵∠CAB=∠EAD=90°,
∴∠CAE=∠BAD.
在△CAE和△BAD中,
 ,
,
∴△CAE≌△BAD(SAS),
∴CE=BD
(2)证明:延长BD交CE于F,如图所示:
∵△CAE≌△BAD,
∴∠ACE=∠ABD,
∵∠CAB=90°,
∴∠ABC+∠ACB=90°,
即∠ABD+∠DBC+∠ACB=90°,
∴∠DBC+∠ACB+∠ACE=90°,
即∠DBC+∠BCF=90°,
∴∠BFC=90°,
∴CE⊥BD.

【解析】(1)由已知条件证出∠CAE=∠BAD,由SAS证明△CAE≌△BAD,得出对应边相等即可;(2)延长BD交CE于F,由全等三角形的性质得出∠ACE=∠ABD,由角的互余关系得出∠ABC+∠ACB=90°,证出∠DBC+∠BCF=90°,得出∠BFC=90°即可.

练习册系列答案
相关题目