Question

【题目】如图，AC⊥x轴于点A，点B在y轴的正半轴上，∠ABC=60°，AB=4，BC=2 ，点D为AC与反比例函数y= 的图象的交点．若直线BD将△ABC的面积分成1：2的两部分，则k的值为 ．

Answer 1

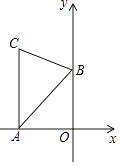
【答案】﹣4或﹣8
【解析】解：如图所示，过C作CE⊥AB于E，

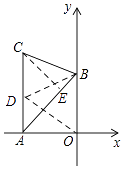
∵∠ABC=60°，BC=2 ，

∴Rt△CBE中，CE=3，

又∵AC=4，

∴△ABC的面积= AB×CE= ×4×3=6，

连接BD，OD，

∵直线BD将△ABC的面积分成1：2的两部分，

∴点D将线段AC分成1：2的两部分，

当AD：CD=1：2时，△ABD的面积= ×△ABC的面积=2，

∵AC∥OB，

∴△DOA的面积=△ABD的面积=2，

∴ |k|=2，即k=±4，

又∵k＜0，

∴k=﹣4；

当AD：CD=2：1时，△ABD的面积= ×△ABC的面积=4，

∵AC∥OB，

∴△DOA的面积=△ABD的面积=4，

∴ |k|=4，即k=±8，

又∵k＜0，

∴k=﹣8，

所以答案是：﹣4或﹣8．