题目内容
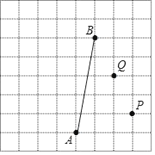
【题目】在下列网格中，每个小正方形的边长都是1，点A、B、P、Q均为格点．
(Ⅰ)线段AB的长度等于__________；
(Ⅱ)点M、N是线段AB上的两个动点(M较靠近点B)，且始终满足
，若点M、N运动恰好使四边形MNPQ的周长最小时，请在给定的网格中用无刻度直尺画出点M的位置，并简要说明你的作图方法：__________．
【答案】
取格点PP′，使得PP′∥AB，在PP′上截取
，作G关于AB的对称点R，连接QR交AB于点M，点M即为所求
【解析】
(Ⅰ)根据勾股定理计算即可；
(Ⅱ)取格点PP′，使得PP′∥AB，在PP′上截取，作G关于AB的对称点R，连接QR交AB于点M，点M即为所求．
解：(Ⅰ)由勾股定理得：
．
故答案为
(Ⅱ)取格点P′，C，C′，D，D′，连接CC′交格线于E，连接DD′交格线于F，连接EF交PP′于G，此时；
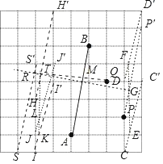
取格点H，H′，I，I′，J，J′，连接II′交格线于K，连接JJ′交格线于L，延长KL与HH′交于点T，取格点S，S′，延长GT交SS′于点R，连接RQ交AB于点M，
点M即为所求．
故答案为取格点PP′，使得PP′∥AB，在PP′上截取，作G关于AB的对称点R，连接QR交AB于点M，点M即为所求．
练习册系列答案
快乐5加2金卷系列答案
相关题目
