题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.
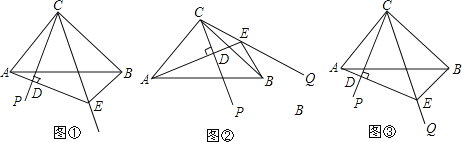
(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;
(2)如图②,当CQ在∠ACB外部时,求证AD-BE=DE;
(3)在(1)的条件下,若CD=18,S△BCE=2S△ACD,求AE的长.(直接写结果)
【答案】(1)见解析;(2)见解析;(3)24
【解析】试题分析:(1)延长DA到F,使DF=DE,根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得证;
(2)在AD上截取DF=DE,然后根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得到AD=BE+DE;
(3)根据等腰直角三角形的性质求出CD=DF=DE,再根据等高的三角形的面积的比等于底边的比求出AF=2AD,然后求出AD的长,再根据AE=AD+DE代入数据进行计算即可得解.
试题解析:
(1)如图①,延长DA到F,使DF=DE,
∵CD⊥AE,∴CE=CF,
∴∠DCE=∠DCF=∠PCQ=45°,
∴∠ACD+∠ACF=∠DCF=45°,
又∵∠ACB=90°,∠PCQ=45°,
∴∠ACD+∠BCE=90°-45°=45°,
∴∠ACF=∠BCE,
∵在△ACF和△BCE中, 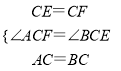 ,
,
∴△ACF≌△BCE(SAS),∴AF=BE,
∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
(2)如图②,在AD上截取DF=DE,
∵CD⊥AE,∴CE=CF,
∴∠DCE=∠DCF=∠PCQ=45°,
∴∠ECF=∠DCE+∠DCF=90°,
∴∠BCE+∠BCF=∠ECF=90°,
又∵∠ACB=90°,∴∠ACF+∠BCF=90°,∴∠ACF=∠BCE,
∵在△ACF和△BCE中, 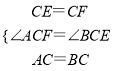 ,
,
∴△ACF≌△BCE(SAS),∴AF=BE,
∴AD=AF+DF=BE+DE,即AD=BE+DE;
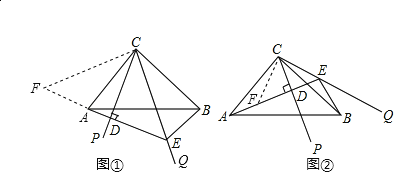
(3)∵∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=45°+45°=90°,
∴△ECF是等腰直角三角形,∴CD=DF=DE=6,
∵S△BCE=2S△ACD,∴AF=2AD,
∴AD=![]() ×6=2,∴AE=AD+DE=2+6=8.
×6=2,∴AE=AD+DE=2+6=8.