��Ŀ����
��ͼ��ʾ���߳�Ϊ2��������OABC��ͼ������ƽ��ֱ������ϵ�У�������y=ax2+bx+c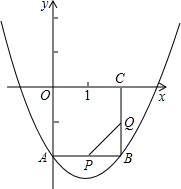 ����A��B����12a+5c=0��
����A��B����12a+5c=0����1���������ߵĽ���ʽ��
��2�������P�ɵ�A��ʼ��AB����ÿ��2����λ���ٶ����B�ƶ���ͬʱ��Q�ɵ�B��ʼ��BC����ÿ��1����λ���ٶ����C�ƶ������ƶ�ʱ��Ϊt�룮���߶�PQ�ij�ȡ����Сֵʱ�������������Ƿ���ڵ�R��ʹ����P��B��Q��RΪ������ı���Ϊƽ���ı��Σ�����ڣ������R�����ꣻ�粻���ڣ���˵�����ɣ�
��3���ڣ�2���������£�P��Q�����˶������У����������Ƿ���������R��ʹ����P��B��Q��RΪ������ı���Ϊƽ���ı��Σ�����ڣ������R�����ꣻ�粻���ڣ���˵�����ɣ�
��������1�����������εı߳��ɵ�A��B��������꣬�����Ǵ��������ߵĽ���ʽ�У�����12a+5c=0��������ô���ϵ����ֵ���Ӷ�ȷ���������ߵĽ���ʽ��
��2��������t��ʾ��PB��BQ�ij������ù��ɶ��������PQ2�ı���ʽ���������ú��������ʼ��ɵõ�PQ2����Сֵ����PQ����Сֵ������Ӧ��tֵ�������ɵõ�P��Q�����꣬Ȼ�������������ǣ�
��PR��BQƽ������ȣ���ô��P���������ϻ�����ƽ��BQ����λ�����ɵõ�R�����꣬Ȼ������������ߵĽ���ʽ�н�����֤���ɣ�
��QR��BPƽ������ȣ���ô��Q���������������ƽ��BP����λ���ɵõ�R�����꣬Ȼ������������ߵĽ���ʽ�н�����֤���ɣ�
��3������Ľⷨͬ��2������P��Q��������t��ʾ��Ȼ��2�������������õ����Ե�R�����꣬Ȼ���ٴ����������н�����֤���ɣ�
��2��������t��ʾ��PB��BQ�ij������ù��ɶ��������PQ2�ı���ʽ���������ú��������ʼ��ɵõ�PQ2����Сֵ����PQ����Сֵ������Ӧ��tֵ�������ɵõ�P��Q�����꣬Ȼ�������������ǣ�
��PR��BQƽ������ȣ���ô��P���������ϻ�����ƽ��BQ����λ�����ɵõ�R�����꣬Ȼ������������ߵĽ���ʽ�н�����֤���ɣ�
��QR��BPƽ������ȣ���ô��Q���������������ƽ��BP����λ���ɵõ�R�����꣬Ȼ������������ߵĽ���ʽ�н�����֤���ɣ�
��3������Ľⷨͬ��2������P��Q��������t��ʾ��Ȼ��2�������������õ����Ե�R�����꣬Ȼ���ٴ����������н�����֤���ɣ�
��� �⣺��1������A��0��-2����B��2��-2����
�⣺��1������A��0��-2����B��2��-2����
��
��
��y=
x2-
x-2����4�֣�
��2������AP=2t��BQ=t��
��BP=2-2t��
Rt��PBQ��
PQ2=PB2+BQ2=��2-2t��2+t2
=5t2-8t+4
=5(t-
)2+
��
��t=
ʱ��PQ2ȡ����Сֵ��
��PQ��С����ʱP(
��-2)��Q(2��-
)��
������������ĵ�R���ڣ�
�ٹ�P��PR��BQ��PR=BQ��
��ʱR��
��-
����(
��-
)��
������������߽���ʽ��
֪��������R�������������ϣ�
�ڹ�Q��QR��BP��QR=BP��
��ʱR��
��-
����(
��-
)������������߽���ʽ��
֪�㣨
��-
�����������ϣ���(
��-
)�����������ϣ�
�������������ڷ��������ĵ�R��
��-
������8�֣�
��3����֪��P��2t��-2����Q��2��t-2����
���ڵ�R���������ϣ�
����������P��B��Q��RΪ�����ƽ���ı��Σ�ֻ�������������
��ƽ���ı���PRBQ��ʱPR��BQ��PR=BQ��
��R��2t��-2-t����
������������߽���ʽ�ã�
•(2t)2-
•2t-2=-2-t��
10t2-7t=-0��
t1=0(��ȥ)t2=
��
��ʱR(
��-
)��
��PQRB����ʱQR��PB��QR=PB��
��R��4-2t��t-2����
������������߽���ʽ��
(4-2t)2-
(4-2t)-2=t-2��
10t2-33t+20=0��
��t1=2.5����ȥ����t2=0.8��
��ʱR��
��-
����
��������������2���еĵ�R�⣬�����ڵ�R(
��-
)����12�֣�
 �⣺��1������A��0��-2����B��2��-2����
�⣺��1������A��0��-2����B��2��-2������
|
��
|
��y=
| 5 |
| 6 |
| 5 |
| 3 |
��2������AP=2t��BQ=t��
��BP=2-2t��
Rt��PBQ��
PQ2=PB2+BQ2=��2-2t��2+t2
=5t2-8t+4
=5(t-
| 4 |
| 5 |
| 4 |
| 5 |
��t=
| 4 |
| 5 |
��PQ��С����ʱP(
| 8 |
| 5 |
| 6 |
| 5 |
������������ĵ�R���ڣ�
�ٹ�P��PR��BQ��PR=BQ��
��ʱR��
| 8 |
| 5 |
| 14 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
������������߽���ʽ��
֪��������R�������������ϣ�
�ڹ�Q��QR��BP��QR=BP��
��ʱR��
| 12 |
| 5 |
| 6 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
֪�㣨
| 12 |
| 5 |
| 6 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
�������������ڷ��������ĵ�R��
| 12 |
| 5 |
| 6 |
| 5 |
��3����֪��P��2t��-2����Q��2��t-2����
���ڵ�R���������ϣ�
����������P��B��Q��RΪ�����ƽ���ı��Σ�ֻ�������������
��ƽ���ı���PRBQ��ʱPR��BQ��PR=BQ��
��R��2t��-2-t����
������������߽���ʽ�ã�
| 5 |
| 6 |
| 5 |
| 3 |
10t2-7t=-0��
t1=0(��ȥ)t2=
| 7 |
| 10 |
��ʱR(
| 7 |
| 5 |
| 27 |
| 10 |
��PQRB����ʱQR��PB��QR=PB��
��R��4-2t��t-2����
������������߽���ʽ��
| 5 |
| 6 |
| 5 |
| 3 |
10t2-33t+20=0��
��t1=2.5����ȥ����t2=0.8��
��ʱR��
| 12 |
| 5 |
| 6 |
| 5 |
��������������2���еĵ�R�⣬�����ڵ�R(
| 7 |
| 5 |
| 27 |
| 10 |
������������Ҫ�����˶��κ�������ʽ��ȷ���������ε����ʡ�ƽ���ı��ε��ж������ʡ�����ͼ���ϵ�����������֪ʶ�����漰����������ʱ��һ��Ҫע���������˼���Ӧ�ã�����©�⣮

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��ʾ���߳�Ϊ1��С�����ι��ɵ������У��뾶Ϊ1�ġ�O��Բ��O�ڸ���ϣ���tan��AED��ֵ���ڣ�������
��ͼ��ʾ���߳�Ϊ1��С�����ι��ɵ������У��뾶Ϊ1�ġ�O��Բ��O�ڸ���ϣ���tan��AED��ֵ���ڣ�������A��
| ||||
B��
| ||||
C��
| ||||
D��
|
 ��ͼ��ʾ���߳�Ϊ1��С�����ι��ɵ������У��뾶Ϊ1�ġ�O��Բ��O�ڸ���ϣ����AED������ֵ����
��ͼ��ʾ���߳�Ϊ1��С�����ι��ɵ������У��뾶Ϊ1�ġ�O��Բ��O�ڸ���ϣ����AED������ֵ���� ����OAB�Ƶ�O˳ʱ����ת30��õ���OB��A�䣬��A��ǡ������˫����y=
����OAB�Ƶ�O˳ʱ����ת30��õ���OB��A�䣬��A��ǡ������˫����y= 23����Ϊ50cm�������ܳ�Ϊ50cm��Բ�����ڴ�Բ���IJ����ϻ��֣���ͼ��ʾ���߳�Ϊlcm�������Σ����ĸ��߳�Ϊlcm��С�����ι��ɡ�T�����Σ��ô�ͼ���Ƿ���ƴ��Բ�����棿��˵�����ɣ�
23����Ϊ50cm�������ܳ�Ϊ50cm��Բ�����ڴ�Բ���IJ����ϻ��֣���ͼ��ʾ���߳�Ϊlcm�������Σ����ĸ��߳�Ϊlcm��С�����ι��ɡ�T�����Σ��ô�ͼ���Ƿ���ƴ��Բ�����棿��˵�����ɣ� ��ͼ��ʾ���߳�Ϊ1 ���������������и���ABC�������������ߵĽ��㣩���O�����ѡ�ABC�Ƶ�O��ʱ����ת90�㣮
��ͼ��ʾ���߳�Ϊ1 ���������������и���ABC�������������ߵĽ��㣩���O�����ѡ�ABC�Ƶ�O��ʱ����ת90�㣮