题目内容
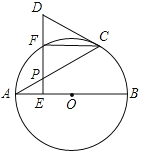
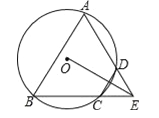
【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据圆内接四边形的性质得到∠A=∠DCE,根据等腰三角形的性质得到∠DCE=∠DEC,等量代换证明结论;
(2)根据垂径定理得到OE是CD的垂直平分线,根据题意证明△DEC为等边三角形,证明结论.
试题解析:(1)∵四边形ABCD是⊙O的内接四边形,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠DEC,∴∠A=∠AEB;
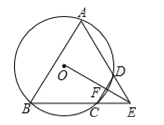
(2)∵DC⊥OE,∴DF=CF,∴OE是CD的垂直平分线,∴ED=EC,又DE=DC,∴△DEC为等边三角形,∴∠AEB=60°,又∠A=∠AEB,∴△ABE是等边三角形.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目