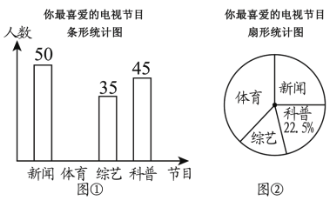
ЬтФПФкШн
ЁОЬтФПЁПзлКЯгыЬНОП
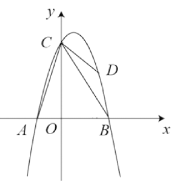
ШчЭМЃЌХзЮяЯп![]() ОЙ§ЕуA(-2,0)ЃЌB(4,0)СНЕуЃЌгы
ОЙ§ЕуA(-2,0)ЃЌB(4,0)СНЕуЃЌгы![]() жсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊ
жсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊ![]() .СЌНгACЃЌBCЃЌDBЃЌDCЃЌ
.СЌНгACЃЌBCЃЌDBЃЌDCЃЌ
(1)ЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
(2)ЁїBCDЕФУцЛ§ЕШгкЁїAOCЕФУцЛ§ЕФ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
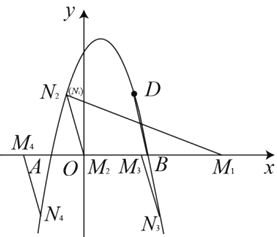
(3)дк(2)ЕФЬѕМўЯТЃЌШєЕуMЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдХаЖЯЪЧЗёДцдкетбљЕФЕуM,ЪЙЕУвдЕуBЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
жсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдХаЖЯЪЧЗёДцдкетбљЕФЕуM,ЪЙЕУвдЕуBЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁП(1)![]() ЃЛ(2)3ЃЛ(3)
ЃЛ(2)3ЃЛ(3)![]() .
.
ЁОНтЮіЁП
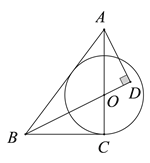
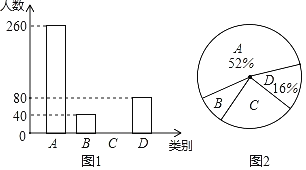
(1)РћгУД§ЖЈЯЕЪ§ЗЈНјааЧѓНтМДПЩЃЛ
(2)зїжБЯпDEЁЭ![]() жсгкЕуEЃЌНЛBCгкЕуGЃЌзїCFЁЭDEЃЌДЙзуЮЊFЃЌЯШЧѓГіSЁїOAC=6ЃЌдйИљОнSЁїBCD=
жсгкЕуEЃЌНЛBCгкЕуGЃЌзїCFЁЭDEЃЌДЙзуЮЊFЃЌЯШЧѓГіSЁїOAC=6ЃЌдйИљОнSЁїBCD=![]() SЁїAOCЃЌЕУЕНSЁїBCD =
SЁїAOCЃЌЕУЕНSЁїBCD =![]() ЃЌШЛКѓЧѓГіBCЕФНтЮіЪНЮЊ
ЃЌШЛКѓЧѓГіBCЕФНтЮіЪНЮЊ![]() ЃЌдђПЩЕУЕуGЕФзјБъЮЊ
ЃЌдђПЩЕУЕуGЕФзјБъЮЊ![]() ЃЌгЩДЫПЩЕУ
ЃЌгЩДЫПЩЕУ![]() ЃЌдйИљОнSЁїBCD=SЁїCDG+SЁїBDG=
ЃЌдйИљОнSЁїBCD=SЁїCDG+SЁїBDG=![]() ЃЌПЩЕУЙигкmЕФЗНГЬЃЌНтЗНГЬМДПЩЧѓЕУД№АИЃЛ
ЃЌПЩЕУЙигкmЕФЗНГЬЃЌНтЗНГЬМДПЩЧѓЕУД№АИЃЛ
(3)ДцдкЃЌШчЯТЭМЫљЪОЃЌвдBDЮЊБпЛђепвдBDЮЊЖдНЧЯпНјааЦНааЫФБпаЮЕФЙЙЭМЃЌвдBDЮЊБпЪБЃЌга3жжЧщПіЃЌгЩЕуDЕФзјБъПЩЕУЕуNЕузнзјБъЮЊЁР![]() ЃЌШЛКѓЗжЕуNЕФзнзјБъЮЊ
ЃЌШЛКѓЗжЕуNЕФзнзјБъЮЊ![]() КЭЕуNЕФзнзјБъЮЊ
КЭЕуNЕФзнзјБъЮЊ![]() СНжжЧщПіЗжБ№ЧѓНтЃЛвдBDЮЊЖдНЧЯпЪБЃЌга1жжЧщПіЃЌДЫЪБN1ЕугыN2ЕужиКЯЃЌИљОнЦНааЫФБпаЮЕФЖдБпЦНааЧвЯрЕШПЩЧѓЕУBM1=N1D=4ЃЌМЬЖјЧѓЕУOM1= 8ЃЌгЩДЫМДПЩЧѓЕУД№АИ.
СНжжЧщПіЗжБ№ЧѓНтЃЛвдBDЮЊЖдНЧЯпЪБЃЌга1жжЧщПіЃЌДЫЪБN1ЕугыN2ЕужиКЯЃЌИљОнЦНааЫФБпаЮЕФЖдБпЦНааЧвЯрЕШПЩЧѓЕУBM1=N1D=4ЃЌМЬЖјЧѓЕУOM1= 8ЃЌгЩДЫМДПЩЧѓЕУД№АИ.
(1)ХзЮяЯп![]() ОЙ§ЕуA(-2,0)ЃЌB(4,0)ЃЌ
ОЙ§ЕуA(-2,0)ЃЌB(4,0)ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ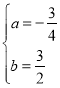 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊ![]() ЃЛ
ЃЛ
(2)зїжБЯпDEЁЭ![]() жсгкЕуEЃЌНЛBCгкЕуGЃЌзїCFЁЭDEЃЌДЙзуЮЊFЃЌ
жсгкЕуEЃЌНЛBCгкЕуGЃЌзїCFЁЭDEЃЌДЙзуЮЊFЃЌ
ЁпЕуAЕФзјБъЮЊ(-2,0)ЃЌЁрOA=2ЃЌ
гЩ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЁрЕуCЕФзјБъЮЊ(0,6)ЃЌЁрOC=6ЃЌ
ЃЌЁрЕуCЕФзјБъЮЊ(0,6)ЃЌЁрOC=6ЃЌ
ЁрSЁїOAC=![]() ЃЌ
ЃЌ
ЁпSЁїBCD=![]() SЁїAOCЃЌ
SЁїAOCЃЌ
ЁрSЁїBCD =![]() ЃЌ
ЃЌ
ЩшжБЯпBCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЌ
ЃЌ
гЩBЃЌCСНЕуЕФзјБъЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ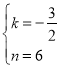 ЃЌ
ЃЌ
ЁржБЯпBCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЌ
ЃЌ
ЁрЕуGЕФзјБъЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЕуBЕФзјБъЮЊ(4,0)ЃЌЁрOB=4ЃЌ
ЁпSЁїBCD=SЁїCDG+SЁїBDG=![]() ЃЌ
ЃЌ
ЁрSЁїBCD =![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() (Щс)ЃЌ
(Щс)ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЕФжЕЮЊ3ЃЛ
ЕФжЕЮЊ3ЃЛ
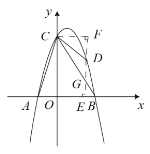
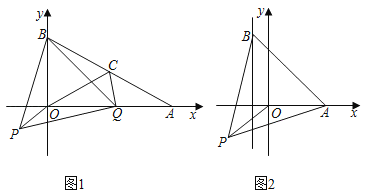
(3)ДцдкЃЌШчЯТЭМЫљЪОЃЌвдBDЮЊБпЛђепвдBDЮЊЖдНЧЯпНјааЦНааЫФБпаЮЕФЙЙЭМЃЌ
вдBDЮЊБпЪБЃЌга3жжЧщПіЃЌ
ЁпDЕузјБъЮЊ![]() ЃЌЁрЕуNЕузнзјБъЮЊЁР
ЃЌЁрЕуNЕузнзјБъЮЊЁР![]() ЃЌ
ЃЌ
ЕБЕуNЕФзнзјБъЮЊ![]() ЪБЃЌШчЕуN2ЃЌ
ЪБЃЌШчЕуN2ЃЌ
ДЫЪБ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() (Щс)ЃЌ
(Щс)ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЛ
ЃЛ
ЕБЕуNЕФзнзјБъЮЊ![]() ЪБЃЌШчЕуN3ЃЌN4ЃЌ
ЪБЃЌШчЕуN3ЃЌN4ЃЌ
ДЫЪБ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]()
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
вдBDЮЊЖдНЧЯпЪБЃЌга1жжЧщПіЃЌДЫЪБN1ЕугыN2ЕужиКЯЃЌ
Ёп![]() ЃЌD(3ЃЌ
ЃЌD(3ЃЌ![]() )ЃЌ
)ЃЌ
ЁрN1D=4ЃЌ
ЁрBM1=N1D=4ЃЌ
ЁрOM1=OB+BM1=8ЃЌ
ЁрM1(8ЃЌ0)ЃЌ
злЩЯЃЌЕуMЕФзјБъЮЊЃК![]() .
.