题目内容
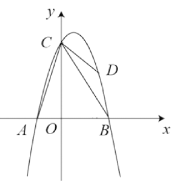
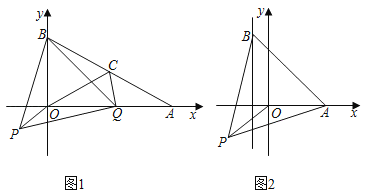
【题目】(1)问题发现:如图1,在平面直角坐标系中,A点的坐标为(2![]() ,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:
,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:
①OP与CQ的大小关系是 .
②OP的最小值为 .
(2)解决问题:在(1)的条件下,点Q运动的过程中当△ACQ为直角三角形时,求OP的长?
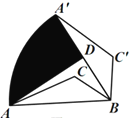
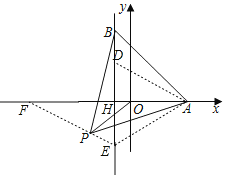
(3)拓展探究:如图2,当点B为直线x=﹣1上一动点,点A(2![]() ,0),连接AB,以AB为一边向下作等边△ABP,连接OP,请直接写出OP的最小值.
,0),连接AB,以AB为一边向下作等边△ABP,连接OP,请直接写出OP的最小值.
【答案】(1)①OP=CQ;②1;(2)OP的长为1或![]() ;(3)OP的最小值为
;(3)OP的最小值为![]() +1
+1
【解析】
(1)①证明△OBC是等边三角形,得出OB=BC,证明△PBO≌△QBC(SAS),可得出结论;
②当CQ⊥OA时,CQ值最小,得出最小值为![]() OB=1;
OB=1;
(2)分两种情况:①以Q点为直角顶点时,CQ⊥AO于点Q,②以C点为直角顶点时,CQ⊥AC,由直角三角形的性质可得出答案;
(3)以OA为对称轴,在x=﹣1上取D,E两点,作等边△ADE,连接EP,并延长EP交x轴于点F.证明△AEP≌△ADB(SAS),得出∠AEP=∠ADB=120°,可求出HF,OF,当OP⊥EF时,OP最小,则OP=![]() OF=
OF=![]() .
.
解:(1)问题发现
①∵A点的坐标为(2![]() ,0),点B的坐标为(0,2),
,0),点B的坐标为(0,2),
∴OA=2![]() ,OB=2,
,OB=2,
![]() ,
,
∴∠OBA=60°,
![]()
∵C是AB的中点,
![]()
∴OB=OC,
∴△OBC是等边三角形,
∴OB=BC,
∵△BPQ是等边三角形,
∴PB=BQ,∠PBQ=60°,
∴∠PBO=∠QBC,
∴△PBO≌△QBC(SAS),
∴OP=CQ,
②∵C是AB的中点,
∴CQ⊥OA时,CQ值最小,最小值为![]() OB=1,
OB=1,
∴OP的最小值为1.
故答案为:OP=CQ;1;
(2)解决问题
当三角形ACQ为直角三角形时,
①以Q点为直角顶点时,CQ⊥AO于点Q,
∵C为AB的中点,
∴AC=![]() ,
,
∴CQ=![]() AC=1,
AC=1,
即OP=1,
②以C点为直角顶点时,CQ⊥AC,
∵AC=2,
∴CQ=ACtan30°=2span>×![]() =
=![]() .
.
即OP=![]() .
.
综上所述:当三角形ACQ为直角三角形时,OP的长为1或![]() ;
;
(3)拓展探究
如图,以OA为对称轴,在x=﹣1上取D,E两点,作等边△ADE,连接EP,并延长EP交x轴于点F.
在△AEP与△ADB中,
∵AB=AP,∠BAD=∠PAE,AD=AE,
∴△AEP≌△ADB(SAS),
∴∠AEP=∠ADB=120°,
∴∠HEF=60°,且EH⊥AF,
∴HF=HA=![]() +1,
+1,
∴FO=FH+OH=![]() +2.
+2.
∴点P在直线EF上运动,
当OP⊥EF时,OP最小,
∴OP=![]() OF=
OF=![]() ,
,
则OP的最小值为![]() +1.
+1.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案