题目内容
三角形两边长为6和8,第三边是方程x2-16x+60=0的根,则该三角形的面积是( )
| A.24 | B.24或8
| C.48 | D.8 |
∵x2-16x+60=0,
∴(x-10)(x-6)=0,
解得:x1=10,x2=6,
∵三角形两边长为6和8,
当x=10时,
∵102=62+82,
∴此三角形是直角三角形,
∴该三角形的面积是:
×6×8=24;
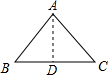
当x=6时,设AB=AC=6,BC=8,
过点A作AD⊥BC于D,
∴BD=
BA=4,
∴AD=
=2
,
∴S△ABC=
×BC×AD=
×8×2
=8
.
∴该三角形的面积是24或8
.
故选B.
∴(x-10)(x-6)=0,
解得:x1=10,x2=6,
∵三角形两边长为6和8,
当x=10时,
∵102=62+82,
∴此三角形是直角三角形,
∴该三角形的面积是:
| 1 |
| 2 |
当x=6时,设AB=AC=6,BC=8,
过点A作AD⊥BC于D,
∴BD=
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
| 5 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∴该三角形的面积是24或8
| 5 |
故选B.


练习册系列答案
相关题目