题目内容
【题目】某“爱心义卖”活动中,购进甲、乙两种文具,甲每个进货价高于乙进货价10元,90元买乙的数量与150元买甲的数量相同.
(1)求甲、乙进货价;
(2)甲、乙共100件,将进价提高20%进行销售,进货价少于2080元,销售额要大于2460元,求有几种方案?
【答案】(1)甲进货价为25元,乙进货价15元;(2)有两种方案:进甲种文具56件,乙种文具44件;进甲种文具57件,乙种文具43件.
【解析】试题分析:(1)由甲每个进货价高于乙进货价10元,设乙进货价x元,则甲进货价为(x+10)元,根据90元买乙的数量与150元买甲的数量相同列出方程解决问题.
(2)由(1)中的数值,求得提高20%的售价,设进甲种文具m件,则乙种文具(100﹣m)件,根据进货价少于2080元,销售额要大于2460元,列出不等式组解决问题.
试题解析:解:(1)设乙进货价x元,则甲进货价为(x+10)元,由题意得
![]() ,解得x=15.
,解得x=15.
经检验x=15是原方程的根.
∴x+10=25.
答:甲进货价为25元,乙进货价15元.
(2)设进甲种文具m件,则乙种文具(100﹣m)件,由题意得
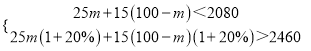 ,解得55<m<58.
,解得55<m<58.
∵m为整数,∴m=56,57,100﹣m=44,43.
∴有两种方案:进甲种文具56件,乙种文具44件;进甲种文具57件,乙种文具43件.

练习册系列答案
相关题目