题目内容
如图,在Rt△ABC中,∠C=90°,CDEF为内接正方形,若AE=2cm,BE=1cm,则图中阴影部分的面积为

A、1cm2; B、 cm2; C、
cm2; C、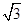 cm2; D、2cm2.
cm2; D、2cm2.

A、1cm2; B、
 cm2; C、
cm2; C、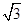 cm2; D、2cm2.
cm2; D、2cm2.A
分析:根据题意分析可得△ADE∽△EFB,进而可得DE=2BF,AD=2EF=2DE,由勾股定理得,DE2+AD2=AE2,可解得DE、EF、AD、BF的长,进而可得阴影部分的面积.
解:根据题意,易得△ADE∽△EFB,
∴BE:AE=BF:DE=EF:AD=1:2,
∴DE=2BF,AD=2EF=2DE,
由勾股定理得,DE2+AD2=AE2,
解得:DE=EF=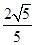 ,AD=
,AD=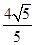 ,BF=
,BF=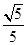 ,
,
故S阴影=S△BFE+S△ADE=1cm2,故答案为A.
解:根据题意,易得△ADE∽△EFB,
∴BE:AE=BF:DE=EF:AD=1:2,
∴DE=2BF,AD=2EF=2DE,
由勾股定理得,DE2+AD2=AE2,
解得:DE=EF=
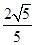 ,AD=
,AD=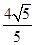 ,BF=
,BF=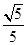 ,
,故S阴影=S△BFE+S△ADE=1cm2,故答案为A.

练习册系列答案
相关题目

 的位似图形.
的位似图形. ,并求出
,并求出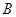 点坐标;
点坐标;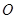 为位似中心,相似比为2:1,在第一象限内将
为位似中心,相似比为2:1,在第一象限内将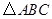 放大,画出放大后的图形
放大,画出放大后的图形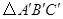 ;
;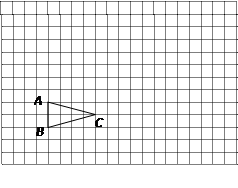
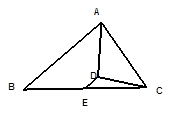
 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2. E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设 ,
, ,
, 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域; 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
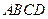 中,
中,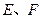 分别是边
分别是边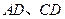 上的点,
上的点,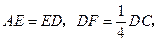 连结
连结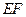 并延长交
并延长交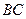 的延长线于点
的延长线于点
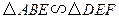 ;
;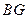 的长.
的长.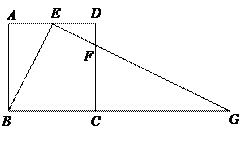
 的AB,AC边上的点,
的AB,AC边上的点, .
.