题目内容
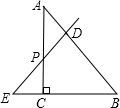 如下图,Rt△ABC中,过直角边AC上的一点P,作直线DE交AB于D,交BC的延长线于E,若∠DPA=∠A,则D点在
如下图,Rt△ABC中,过直角边AC上的一点P,作直线DE交AB于D,交BC的延长线于E,若∠DPA=∠A,则D点在
- A.BC的垂直平分线上
- B.BE的垂直平分线上
- C.AC的垂直平分线上
- D.以上答案都不对
B
分析:根据等角的余角相等,可得∠E=∠B,根据等角对等边,得DE=BD,再根据线段垂直平分线性质的逆定理,知点D在BE的垂直平分线上.
解答:∵∠ACB=90°,
∴∠A+∠B=90°,∠E+∠CPE=90°.
又∠DPA=∠A,∠DPA=∠CPE,
∴∠E=∠B.
∴DE=BD.
则点D在BE的垂直平分线上.
故选B.
点评:此题考查了等角的余角相等的性质、等角对等边的性质以及线段垂直平分线定理的逆定理:和线段两个断点距离相等的点一定在线段的垂直平分线上.
分析:根据等角的余角相等,可得∠E=∠B,根据等角对等边,得DE=BD,再根据线段垂直平分线性质的逆定理,知点D在BE的垂直平分线上.
解答:∵∠ACB=90°,
∴∠A+∠B=90°,∠E+∠CPE=90°.
又∠DPA=∠A,∠DPA=∠CPE,
∴∠E=∠B.
∴DE=BD.
则点D在BE的垂直平分线上.
故选B.
点评:此题考查了等角的余角相等的性质、等角对等边的性质以及线段垂直平分线定理的逆定理:和线段两个断点距离相等的点一定在线段的垂直平分线上.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
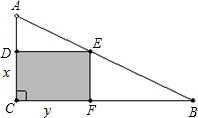 为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池. 8、如下图,Rt△ABC中,过直角边AC上的一点P,作直线DE交AB于D,交BC的延长线于E,若∠DPA=∠A,则D点在( )
8、如下图,Rt△ABC中,过直角边AC上的一点P,作直线DE交AB于D,交BC的延长线于E,若∠DPA=∠A,则D点在( )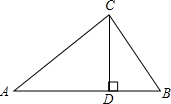 已知:如下图,Rt△ABC中,CD⊥AB于D,AC=4,BC=3,DB=
已知:如下图,Rt△ABC中,CD⊥AB于D,AC=4,BC=3,DB=
 为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.