题目内容
实验学校有一块直角三角形的空地(如下图的Rt△ABC),它的两直角边AC、BC分别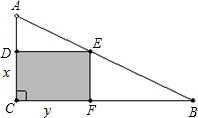 为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.(1)设游泳池相邻两边CD、CF的长分别为x米和y米,求y与x之间的函数关系式;
(2)若建成的游泳池面积为1600平方米,求x和y的值.
分析:(1)根据△ADE∽△ACB,可以列出比例式
=
,代入数据即可求得两者之间的函数关系;
(2)利用矩形的面积计算方法得到x(120-2x)=1600,解得x后代入求得y的值即可.
| AD |
| AC |
| DE |
| CB |
(2)利用矩形的面积计算方法得到x(120-2x)=1600,解得x后代入求得y的值即可.
解答:解:(1)∵三角形ABC为直角三角形,四边形DEFC是长方形,
∴DE∥CB,
∴
=
,
∵AC、BC分别为60米和120米,CD、CF的长分别为x米和y米,
∴
=
,
即:y=120-2x;
(2)S四边形DEFC=xy=x(120-2x)=1600,
解得x=20或x=40(舍去),
y=120-2x=120-2×20=80,
∴x=20,y=80.
∴DE∥CB,
∴
| AD |
| AC |
| DE |
| CB |
∵AC、BC分别为60米和120米,CD、CF的长分别为x米和y米,
∴
| 60-x |
| 60 |
| y |
| 120 |
即:y=120-2x;
(2)S四边形DEFC=xy=x(120-2x)=1600,
解得x=20或x=40(舍去),
y=120-2x=120-2×20=80,
∴x=20,y=80.
点评:本题考查了相似三角形的应用及一元二次方程的知识,综合性较强,但难度不大.

练习册系列答案
相关题目
 育新中学校园内有一块直角三角形(Rt△ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了一串红,在△ACD区域内种植了鸡冠花,并量得两直角边AB=20m,AC=10m,求一串红与鸡冠花两种花草各种植的面积(提示:利用角平分线的性质)
育新中学校园内有一块直角三角形(Rt△ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了一串红,在△ACD区域内种植了鸡冠花,并量得两直角边AB=20m,AC=10m,求一串红与鸡冠花两种花草各种植的面积(提示:利用角平分线的性质) 为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
