题目内容
已知关于x的方程x2+2px+1=0的两个实数根一个小于1，另一个大于1，则实数p的取值范围是______．
设f（x）=x2+2px+1，
∵关于x的方程x2+2px+1=0有两个实数根，
∴△=4p2-4＞0，
解得：P＞1或P＜-1，
∵关于x的方程x2+2px+1=0开口向上，
∴两个实数根一个大于1，另一个小于1（如草图），
∴f（1）=1+2p+1=2p+2＜0，
∴P＜-1，
∴P的范围是：P＜-1．
∵关于x的方程x2+2px+1=0有两个实数根，
∴△=4p2-4＞0，
解得：P＞1或P＜-1，
∵关于x的方程x2+2px+1=0开口向上，
∴两个实数根一个大于1，另一个小于1（如草图），
∴f（1）=1+2p+1=2p+2＜0，
∴P＜-1，
∴P的范围是：P＜-1．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
的解是 （ ）．
，
，
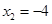
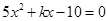的一个根是-5，求它的另一个根是 ，
=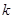