题目内容
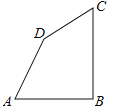
【题目】如图、四边形ABCD中,AB=AD=6,∠A=60°,∠ADC=150°,已知四边形的周长为30,求四边形ABCD的面积.
【答案】9![]() +24.
+24.
【解析】解:连接BD,作DE⊥AB于E,
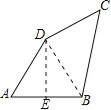
∵AB=AD=6,∠A=60°,
∴△ABD是等边三角形,
∴AE=BE=AB=3,
∴DE=![]() =3,
=3,
因而△ABD的面积是=×ABDE=×6×3=9,
∵∠ADC=150°
∴∠CDB=150°﹣60°=90°,
则△BCD是直角三角形,
又∵四边形的周长为30,
∴CD+BC=30﹣AD﹣AB=30﹣6﹣6=18,
设CD=x,则BC=18﹣x,
根据勾股定理得到62+x2=(18﹣x)2
解得x=8,
∴△BCD的面积是×6×8=24,
S四边形ABCD=S△ABD+S△BDC=9+24.
答:四边形ABCD的面积是9+24.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目