题目内容
在各个内角都相等的多边形中,一个内角是与它相邻的一个外角的3倍,那么这个多边形的边数是
- A.4
- B.6
- C.8
- D.10
C
分析:本题由题意可设这个内角为x,列出方程为x+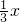 =180°,进而求出此多边形的边数为8.
=180°,进而求出此多边形的边数为8.
解答:∵在这个正多边形中,一个内角等于与它相邻的一个外角的3倍,
则可设这个内角为x,则与它相邻的外角度数为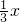 ,
,
∴有x+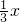 =180°,
=180°,
解得x=135°,则与它相邻的外角度数为45°,
∵360°÷45°=8,
∴这个多边形的边数是8.
故选C.
点评:本题主要考查多边形的外角和定理及邻补角性质.
分析:本题由题意可设这个内角为x,列出方程为x+
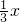 =180°,进而求出此多边形的边数为8.
=180°,进而求出此多边形的边数为8.解答:∵在这个正多边形中,一个内角等于与它相邻的一个外角的3倍,
则可设这个内角为x,则与它相邻的外角度数为
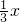 ,
,∴有x+
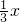 =180°,
=180°,解得x=135°,则与它相邻的外角度数为45°,
∵360°÷45°=8,
∴这个多边形的边数是8.
故选C.
点评:本题主要考查多边形的外角和定理及邻补角性质.

练习册系列答案
相关题目
在各个内角都相等的多边形中,一个外角等于一个内角的
,则这个多边形的边数是( )
| 1 |
| 2 |
| A、5 | B、6 | C、7 | D、8 |
在各个内角都相等的多边形中,一个内角是与它相邻的一个外角的3倍,那么这个多边形的边数是( )
| A、4 | B、6 | C、8 | D、10 |