题目内容
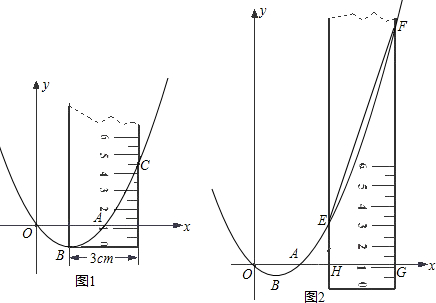
在平面直角坐标系中,抛物线过原点O,且与x轴交于另一点A,其顶点为B.孔明同学用一把宽为3cm带刻度的矩形直尺对抛物线进行如下测量:①量得OA=3cm;
②把直尺的左边与抛物线的对称轴重合,使得直尺左下端点与抛物线的顶点重合(如图1),测得抛物线与直尺右边的交点C的刻度读数为4.5.
请完成下列问题:
(1)写出抛物线的对称轴;
(2)求抛物线的解析式;
(3)将图中的直尺(足够长)沿水平方向向右平移到点A的右边(如图2),直尺的两边交x轴于点H、G,交抛物线于点E、F.求证:S梯形EFGH=
| 1 | 6 |
分析:(1)由于O、A关于抛物线对称轴对称,且OA=3cm,由此可求得抛物线的对称轴为x=
.
(2)根据O、A的坐标,可将抛物线解析式设为交点式,在(1)题求得了抛物线的对称轴,即可得到B、C的横坐标,分别代入抛物线的解析式中,表示出它们的纵坐标,根据C、B的纵坐标差为4.5即可列方程求出待定系数的值,从而确定抛物线的解析式.
(3)可设出E点的横坐标,进而根据直尺的宽度得到F点的横坐标,根据(2)题所得抛物线,即可表示出两点的纵坐标,利用梯形的面积公式,可求出梯形EFGH的面积表达式,然后同
(EF2-9)进行比较即可.
| 3 |
| 2 |
(2)根据O、A的坐标,可将抛物线解析式设为交点式,在(1)题求得了抛物线的对称轴,即可得到B、C的横坐标,分别代入抛物线的解析式中,表示出它们的纵坐标,根据C、B的纵坐标差为4.5即可列方程求出待定系数的值,从而确定抛物线的解析式.
(3)可设出E点的横坐标,进而根据直尺的宽度得到F点的横坐标,根据(2)题所得抛物线,即可表示出两点的纵坐标,利用梯形的面积公式,可求出梯形EFGH的面积表达式,然后同
| 1 |
| 6 |
解答:(1)解:直线x=
;
(2)解:设抛物线的解析式为:y=ax(x-3),
当x=
时,y=-
a,即B(
,-
a);
当x=
时,y=
a,即C(
,
a),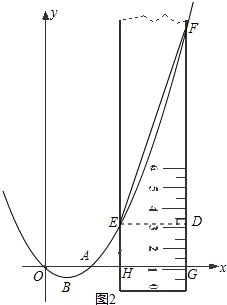
依题意得:
a-(-
a)=4.5,
解得:a=
,
∴抛物线的解析式为:y=
x2-
x;
(3)证明:过点E作ED⊥FG,垂足为D,
设E(x,
x2-
x),
则F(x+3,
x2+
x),
得:S梯形EFGH=
(EH+FG)=
•[(
x2-
x)+(
x2+
x)]=
x2,
∵
(EF2-9)=
×9x2=
x2,
∴S梯形EFGH=
(EF2-9).
| 3 |
| 2 |
(2)解:设抛物线的解析式为:y=ax(x-3),
当x=
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
当x=
| 9 |
| 2 |
| 27 |
| 4 |
| 9 |
| 2 |
| 27 |
| 4 |

依题意得:
| 27 |
| 4 |
| 9 |
| 4 |
解得:a=
| 1 |
| 2 |
∴抛物线的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
(3)证明:过点E作ED⊥FG,垂足为D,
设E(x,
| 1 |
| 2 |
| 3 |
| 2 |
则F(x+3,
| 1 |
| 2 |
| 3 |
| 2 |
得:S梯形EFGH=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∵
| 1 |
| 6 |
| 1 |
| 6 |
| 3 |
| 2 |
∴S梯形EFGH=
| 1 |
| 6 |
点评:此题考查的知识点并不是很多,主要涉及二次函数解析式的确定以及图形面积的求法,能够从图中获得有效的信息是解决问题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.