题目内容
如图,在△ABC中,AB=AC,AD⊥BC于点D,矩形MRTN内接于△ABC(RT在BC边上),正方形EGHF内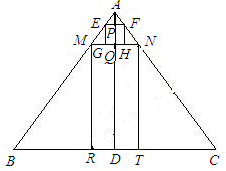 接于△AMN(GH在MN边上),EF,MN分别交AD于点P,Q,设AP=x,已知BC=6,AD=4.
接于△AMN(GH在MN边上),EF,MN分别交AD于点P,Q,设AP=x,已知BC=6,AD=4.(1)试用x的代数式表示线段EF,MN的长;
(2)设S=SEGHF+SMRTN,
①求S关于x的解析式,并写出自变量x的取值范围;
②当x取何值时,S有最大值?
(3)连接RN,当△NRC是等腰三角形时,求x的值.
分析:(1)先根据EF∥BC求出△AEF∽△ABC,根据其相似比可用含x的代数式表示出EF;同理,由MN∥BC,可求出△AMN∽△ABC,根据其相似比为可用含x的代数表示出MN的值;
(2)①由NT=DQ可用含x的代数式表示出NT的长,再结合(1)的结论便可写出S关于x的解析式,根据0<NT<4,即可求出x的取值范围;
②由①求出的函数解析式可判断出a、b的值,根据解析式得出当x取
时,s有的最大值;
(3)由于等腰三角形的两腰不明确,故应分三种情况进行讨论.
(2)①由NT=DQ可用含x的代数式表示出NT的长,再结合(1)的结论便可写出S关于x的解析式,根据0<NT<4,即可求出x的取值范围;
②由①求出的函数解析式可判断出a、b的值,根据解析式得出当x取
| 20 |
| 19 |
(3)由于等腰三角形的两腰不明确,故应分三种情况进行讨论.
解答:解:(1)∵EF∥BC,∴△AEF∽△ABC,
∴
=
即
=
,
∴EF=
x,
又∵MN∥BC,∴△AMN∽△ABC,
∴
=
即
=
,
∴MN=
x;
(2)①∵NT=DQ=AD-AQ=4-(x+
x)=4-
x,
∴S=EF2+MN×NT=(
x)2+
x×(4-
x),
即S=-
x2+15x,
自变量x的取值范围为:0<x<
;
②∵a=-
<0,b=15,
此时x=-
=-
=
,
∵0<
<
,
∴当x=
时,S有最大值;
(3)当△NRC是等腰三角形时,分以下三种情形:
①当NR=NC时,∵NT⊥BC,∴RT=CT,∵DT=
RT=
NM=
x,CD=
BC=3,
∴
x=3-
x,
解得x=
;
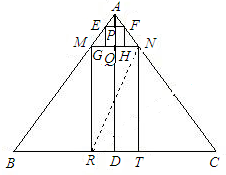 ②当RC=NC时,∵AC=
②当RC=NC时,∵AC=
=
=5,
∴cosC=
=
,
在Rt△NCT中,CT=3-
x∴CN=
=5-
x,
∴
x+3-
x=5-
x,
解得x=
;
③当RC=NR时,
解法一:如图,作RK⊥AC于点K,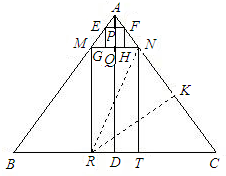
则CK=
CN=
(5-
x),
∵CK=RC×cosC,
∴
(5-
x)=(
x+3-
x)×
,
解得x=
;
解法二:∵RC2=NR2=NT2+RT2,
化简得1075x2-2000x+448=0,
解得x=
,或x=
(不合题意,舍去),
综上所述,当△NRC是等腰三角形时,x=
,或x=
,或x=
.
∴
| EF |
| BC |
| AP |
| AD |
| EF |
| 6 |
| x |
| 4 |
∴EF=
| 3 |
| 2 |
又∵MN∥BC,∴△AMN∽△ABC,
∴
| MN |
| BC |
| AQ |
| AD |
| MN |
| 6 |
x+
| ||
| 4 |
∴MN=
| 15 |
| 4 |
(2)①∵NT=DQ=AD-AQ=4-(x+
| 3 |
| 2 |
| 5 |
| 2 |
∴S=EF2+MN×NT=(
| 3 |
| 2 |
| 15 |
| 4 |
| 5 |
| 2 |
即S=-
| 57 |
| 8 |
自变量x的取值范围为:0<x<
| 8 |
| 5 |
②∵a=-
| 57 |
| 8 |
此时x=-
| b |
| 2a |
| 15 | ||
2×(-
|
| 20 |
| 19 |
∵0<
| 20 |
| 19 |
| 8 |
| 5 |
∴当x=
| 20 |
| 19 |
(3)当△NRC是等腰三角形时,分以下三种情形:
①当NR=NC时,∵NT⊥BC,∴RT=CT,∵DT=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 8 |
| 1 |
| 2 |
∴
| 15 |
| 4 |
| 15 |
| 8 |
解得x=
| 8 |
| 15 |
 ②当RC=NC时,∵AC=
②当RC=NC时,∵AC=| AD2+CD2 |
| 42+32 |
∴cosC=
| CD |
| AC |
| 3 |
| 5 |
在Rt△NCT中,CT=3-
| 15 |
| 8 |
| CT |
| cosC |
| 25 |
| 8 |
∴
| 15 |
| 4 |
| 15 |
| 8 |
| 25 |
| 8 |
解得x=
| 2 |
| 5 |
③当RC=NR时,
解法一:如图,作RK⊥AC于点K,

则CK=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 8 |
∵CK=RC×cosC,
∴
| 1 |
| 2 |
| 25 |
| 8 |
| 15 |
| 4 |
| 15 |
| 8 |
| 3 |
| 5 |
解得x=
| 56 |
| 215 |
解法二:∵RC2=NR2=NT2+RT2,
化简得1075x2-2000x+448=0,
解得x=
| 56 |
| 215 |
| 8 |
| 5 |
综上所述,当△NRC是等腰三角形时,x=
| 8 |
| 15 |
| 2 |
| 5 |
| 56 |
| 215 |
点评:此题比较复杂,涉及到相似三角形判定与性质、二次函数的最值、等腰三角形的性质,在解(2)时一定要注意分类讨论,不要漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=