题目内容
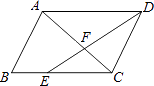
【题目】如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC. 
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
【答案】
(1)证明:∵四边形ABCD为等腰梯形,
∴∠ABE=∠C,且∠BAE=∠DBC,
∴△ABE∽△BCD
(2)解:过D作DG⊥BC于点G,

∵AD=1,BC=3,
∴CG= ![]() (BC﹣AD)=1,BG=2,
(BC﹣AD)=1,BG=2,
又∵在Rt△DGC中,CD=2,CG=1,
∴DG= ![]() ,
,
在Rt△BDG中,tan∠DBC= ![]() =
= ![]()
(3)解:由(2)在Rt△BGD中,由勾股定理可求得BD= ![]() ,
,
由(1)△ABE∽△BCD可得 ![]() =
= ![]() ,即=
,即= ![]() =
= ![]() ,解得BE=
,解得BE= ![]() ,
,
又∵AD∥BC,
∴ ![]() ,且DF=BD﹣BF,
,且DF=BD﹣BF,
∴ ![]() =
= ![]() ,
,
解得BF= ![]()
【解析】(1)根据等腰梯形可得到∠ABE=∠C,结合条件可证得结论;(2)过D作DG⊥BC,则可求得BG、CG,在Rt△DCG中可求得DG,在Rt△BGD中由正切函数的定义可求得tan∠DBC;(3)由(2)可求得BD,结合(1)中的相似可求得BE,再利用平行线分线段成比例得到 ![]() ,代入可求得BF.
,代入可求得BF.

练习册系列答案
相关题目