题目内容
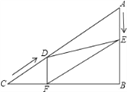
【题目】如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=120°,求∠DCE的度数.
(3)猜想∠ACB和∠DCE的关系,并说明理由;

【答案】(1)145°;(2)60°;(3)∠ACB +∠DCE=180°;理由见解析
【解析】
(1))由∠ACD=∠BCE=90°,根据图形可知∠ACB=180°-∠DCE;
(2)由∠ACD=∠BCE=90°,根据图形可知∠DCE=180°-∠ACB;
(3)由∠ACD=∠BCE=90°,得出∠ACE+∠DCE+∠DCE+∠BCD=180°,即可证出∠ACB+∠DCE=180°.
(1)由题意知:∠ACD=90°,又∠DCE=35° ,
∴∠ACE=∠ACD -∠DCE =90°-35°=55°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°,
(2)若∠ACB=120°,
∴∠ACE=∠ACB -∠BCE =120°-90°=30°,
∴ ∠DCE=∠ACD -∠ACE =90°-30°=60°,
(3)∠ACB +∠DCE=180°;理由如下:
∵∠BCE=∠ACD=90°,
∴∠BCD+∠DCE=90°,∠DCE+∠ACE=90°,
∴∠ACB +∠DCE=∠ACE +∠DCE+BCD+∠DCE=90°+90°=180°.

练习册系列答案
相关题目