Question

已知⊙O的半径为2cm，弦AB的长为2，则这条弦的中点到弦所对优弧的中点的距离为（  ）

A．1cm

B．3cm

C．(2+)cm

D．(2+)cm

Answer 1

B

解析试题分析：画出图形后连接OA，根据垂径定理得出CD过O，AD=BD=cm，OD⊥AB，根据勾股定理求出OD长，即可求出CD．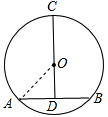

连接OA，
∵D为AB中点，OD过圆心O，C为弧ACB的中点，
∴由垂径定理得：CD过O，AD=BD=cm，OD⊥AB，
∵在△ODA中，OA=2cm，AD=cm，由勾股定理得：OD=1cm，
∴CD=OC+OD=2cm+1cm=3cm，
故选B．
考点：勾股定理和垂径定理的应用
点评：解此题的关键是读懂题意及图形，构造直角三角形后求出OD长，题目比较典型，难度适中．