题目内容
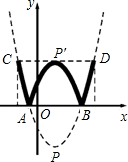 (2012•益阳)已知:如图,抛物线y=a(x-1)2+c与x轴交于点A(1-
(2012•益阳)已知:如图,抛物线y=a(x-1)2+c与x轴交于点A(1-| 3 |
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P'作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比
| ||
| 2 |
| 5 |
| 6 |
分析:(1)利用P与P′(1,3)关于x轴对称,得出P点坐标,利用待定系数法求出二次函数的解析式即可;
(2)根据已知得出C,D两点坐标,进而得出“W”图案的高与宽(CD)的比.
(2)根据已知得出C,D两点坐标,进而得出“W”图案的高与宽(CD)的比.
解答:解:(1)∵P与P′(1,3)关于x轴对称,
∴P点坐标为(1,-3); …(2分)
∵抛物线y=a(x-1)2+c过点A(1-
,0),顶点是P(1,-3),
∴
;…(3分)
解得
;…(4分)
则抛物线的解析式为y=(x-1)2-3,…(5分)
即y=x2-2x-2.
(2)∵CD平行x轴,P′(1,3)在CD上,
∴C、D两点纵坐标为3; …(6分)
由(x-1)2-3=3,
解得:x1=1-
,x2=1+
,…(7分)
∴C、D两点的坐标分别为(1-
,3),(1+
,3)
∴CD=2
…(8分)
∴“W”图案的高与宽(CD)的比=
=
(或约等于0.6124)…(10分).
∴P点坐标为(1,-3); …(2分)
∵抛物线y=a(x-1)2+c过点A(1-
| 3 |
∴
|
解得
|
则抛物线的解析式为y=(x-1)2-3,…(5分)
即y=x2-2x-2.
(2)∵CD平行x轴,P′(1,3)在CD上,
∴C、D两点纵坐标为3; …(6分)
由(x-1)2-3=3,
解得:x1=1-
| 6 |
| 6 |
∴C、D两点的坐标分别为(1-
| 6 |
| 6 |
∴CD=2
| 6 |
∴“W”图案的高与宽(CD)的比=
| 3 | ||
2
|
| ||
| 4 |
点评:此题主要考查了待定系数法求二次函数的解析式以及二次函数的应用,根据已知得出C,D两点坐标是解题关键.

练习册系列答案
相关题目
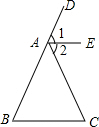 (2012•益阳)如图,已知AE∥BC,AE平分∠DAC.
(2012•益阳)如图,已知AE∥BC,AE平分∠DAC.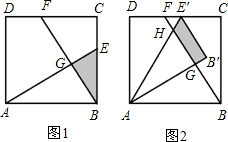 (2012•益阳)已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(2012•益阳)已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.