题目内容
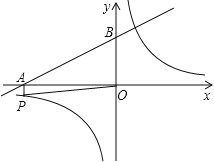
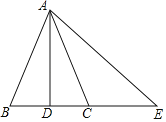
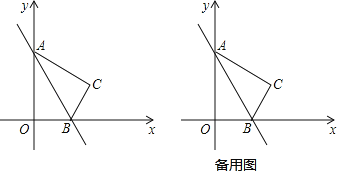
【题目】如图,在坐标平面内,点O是坐标原点,A(0,6),B(2![]() ,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
(1)求点C的坐标:
(2)动点P从点O出发,以2个单位长度/秒的速度沿线段OA向终点A运动,设△POB的面积为S(S≠0),点P的运动时间为t秒,求S与t的关系式,并直接写出t的取值范围.
【答案】(1)C(3![]() ,3);(2)S=2
,3);(2)S=2![]() ,0<t≤3
,0<t≤3
【解析】
(1)图形翻折后对应边长度不变,通过直角三角形中,30°所对的直角边等于斜边一半,依次得出C的坐标.
(2)![]() ,
,![]() 的距离为
的距离为![]() ,
,![]() 可得;另,P的速度为2个单位长度/秒,
可得;另,P的速度为2个单位长度/秒,![]() 则
则![]() 总的时间为
总的时间为![]() .
.
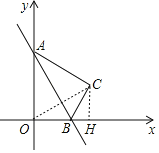
解:(1)连接OC,过C点作CH⊥x轴于H点.
∵折叠![]() ,
,
∴OA=AC,∠OBA=∠CBA=60°,OB=CB,∠CBH=60°
∴![]() 是等边三角形
是等边三角形
∴∠BCH=30°
∴![]() ,
,
∵OC=OA=6,∠COH=30°
∴![]() .
.
∴![]() ;
;
(2)∵点P的运动时间为t秒,
∴OP=2t,
∴![]() .
.
∵点P以2个单位长度/秒的速度沿线段OA向终点A运动,
∴t的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 8 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1),(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.