Question

（1）如果△ABC的面积是S，E是BC的中点，连接AE（图1），则△AEC的面积是

 

；
（2）在△ABC的外部作△ACD，F是AD的中点，连接CF（图2），若四边形ABCD的面积是S，则四边形AECF的面积是

 

；

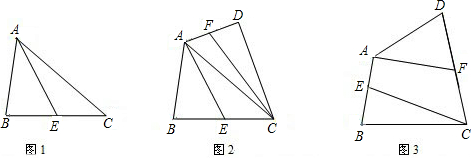
（3）若任意四边形ABCD的面积是S，E、F分别是一组对边AB，CD的中点，连接AF，CE（图3），则四边形AECF的面积是

 

．
拓展与应用
（1）若八边形ABCDEFGH的面积是100，K，M，N，O，P，Q分别是AB，BC，CD，EF，FG，GH的中点，连接KH，MG，NF，OD，PC，QB（图4），则图中阴影部分的面积是

 

；
（2）四边形ABCD的面积是100，E，F分别是一组对边AB，CD上的点，且AE=

1

3

AB，CF=

1

3

CD，连接AF，CE（图5），则四边形AECF的面积是

 

．

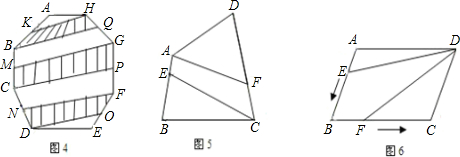
（3）?ABCD的面积为2，AB=a，BC=b，点E从点A出发沿AB以每秒v个单位长的速度向点B运动．点F从点B出发沿BC以每秒

bv

a

个单位的速度向点C运动．E、F分别从点A，B同时出发，当其中一点到达端点时，另一点也随之停止运动．请问四边形DEBF的面积的值是否随着时间t的变化而变化？若不变，请写出这个值

 

，并写出理由；若变化，说明是怎样变化的．

Answer 1

分析：（1）三角形的中线把三角形分为两个面积相等的三角形，其中一个小三角形等于大三角形面积的一半；
（2）由（1）易得构成四边形AECF的两个三角形的面积都等于所在大三角形的面积的一半，那么四边形AECF的面积等于四边形ABCD的面积的一半；
（3）连接AC可得（2）中的图形，那么结论和（2）相同；
拓展与应用
（1）连接BG，CF，那么根据上面得到的结论，阴影部分的面积等于所在的四边形的面积的一半，可得到阴影部分面积之和等于八边形的一半；
（2）连接AC后，△AEC和△BEC的高相等，那么它们面积的比等于底边的边，那么S_△AEC=

1

3

S_△ABC，同理可得S_△AFC=

1

3

S_△ACD，相加后可得阴影部分面积=

1

3

S_{四边形ABCD}；
（3）平行四边形被对角线分得的两个三角形的面积相等．

解答：解：（1）△AEC的面积是

1

2

S；
（2）四边形AECF的面积是

1

2

S；
（3）四边形AECF的面积是

1

2

S．
拓展与应用（1）图中阴影部分的面积是50；
（2）四边形AECF的面积是

100

3

；
（3）这个值是1；连接BD．
∵S_△BED=

a-v

a

S_△ABD，S_△BFD=

bv

ab

S_△BCD．
∴S_△BED+S_△BFD=

a-v

a

S_△ABD+

bv

ab

S_△BCD，
∵S_△ABD=S_△BCD，
∴S_△BED+S_△BFD=S_△ABD=1．

点评：本题主要用到的知识点为：高相等，三角形面积的比就等于底的比．平行四边形被对角线分得的两个三角形的面积相等．