题目内容
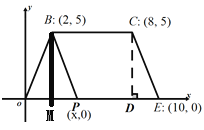
【题目】如图,在平面直角坐标系内,四边形OECB的顶点坐标分别是:B(2,5),C(8,5),E(10,0),点P(x,0)是线段OE上一点,设四边形BPEC的面积为S.

(1)过点C作CD⊥x轴于点E,则CD= , 用含x的代数式表示PE= .
(2)求S与x的函数关系.
(3)当S=30时,直接写出线段PE与PB的长.
【答案】(1)CD=5,PE=10-x;(2)![]() (3)PE=6,PB=
(3)PE=6,PB=![]()
【解析】试题分析:(1)根据点D的坐标直接求得CD的长,根据点E的坐标表示出PE的长即可;(2)根据已知条件可知四边形BPEC是梯形,利用梯形的面积公式即可求解.(2)把S=30 代入![]() 求得x的值,即可求得PE的长,过点B作BM⊥X轴于点M,在Rt△BPM中,根据勾股定理求得PB的长即可.
求得x的值,即可求得PE的长,过点B作BM⊥X轴于点M,在Rt△BPM中,根据勾股定理求得PB的长即可.
试题解析:
(1)CD=5,PE=10-x;
(2)∵B(2,5),C(8,5),
∴BC=6,BC∥x轴,
∴S=![]() .
.
(3)把S=30 代入![]() 得,x=4,
得,x=4,
∴PE=6.
如图,过点B作BM⊥X轴于点M,
∵B(2,5),OP=4,
∴BM=5,PM=2,
在Rt△BPM中,根据勾股定理求得PB=![]() .
.

练习册系列答案
相关题目