题目内容
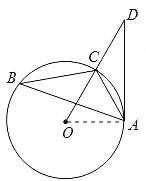
【题目】如图,已知:△ABC内接于⊙O,点D在OC的延长线上,sinB=![]() ,∠D=30度.
,∠D=30度.
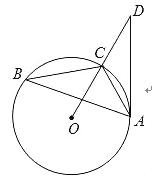
(1)求证:AD是⊙O的切线;
(2)若AC=6,求AD的长.
【答案】(1)AD是⊙O的切线;(2)![]()
【解析】
试题分析:(1)要证明AD是⊙O的切线,只要证明∠OAD=90°即可;
(2)根据已知可得△AOC是等边三角形,从而得到OA=AC=6,则可以利用勾股定理求得AD的长.
试题解析:(1)证明:如图,连接OA;
∵sinB=![]() ,
,
∴∠B=30°,
∵∠AOC=2∠B,
∴∠AOC=60°;
∵∠D=30°,
∴∠OAD=180°﹣∠D﹣∠AOD=90°,
∴AD是⊙O的切线.
(2)解:∵OA=OC,∠AOC=60°,
∴△AOC是等边三角形,
∴OA=AC=6,
∵∠OAD=90°,∠D=30°,
∴AD=![]() AO=
AO=![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目