题目内容
 如图,等腰梯形ABCD中,AD∥BC,AB=DC=5,中位线EF的长为6,则这个等腰梯形的周长为
如图,等腰梯形ABCD中,AD∥BC,AB=DC=5,中位线EF的长为6,则这个等腰梯形的周长为
- A.11
- B.16
- C.17
- D.22
D
分析:由等腰梯形ABCD中,AD∥BC,中位线EF的长为6,根据梯形中位线的性质,即可求得AD+BC的长,又由AB=DC=5,即可求得这个等腰梯形的周长.
解答:∵等腰梯形ABCD中,AD∥BC,中位线EF的长为6,
∴AD+BC=2EF=2×6=12,
∵AB=DC=5,
∴这个等腰梯形的周长为:AB+BC+CD+AD=AB+CD+(AD+BC)=5+5+12=22.
故选D.
点评:此题考查了梯形中位线的性质.此题难度不大,解题的关键是熟练掌握梯形中位线的性质,注意数形结合思想与整体思想的应用.
分析:由等腰梯形ABCD中,AD∥BC,中位线EF的长为6,根据梯形中位线的性质,即可求得AD+BC的长,又由AB=DC=5,即可求得这个等腰梯形的周长.
解答:∵等腰梯形ABCD中,AD∥BC,中位线EF的长为6,
∴AD+BC=2EF=2×6=12,
∵AB=DC=5,
∴这个等腰梯形的周长为:AB+BC+CD+AD=AB+CD+(AD+BC)=5+5+12=22.
故选D.
点评:此题考查了梯形中位线的性质.此题难度不大,解题的关键是熟练掌握梯形中位线的性质,注意数形结合思想与整体思想的应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )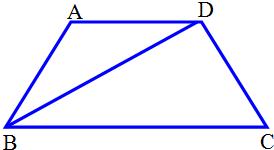 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.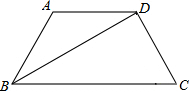 (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=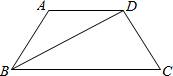 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.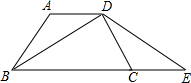 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.