题目内容
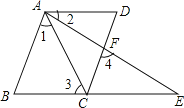
【题目】问题：如图1，在Rt△ABC中，∠C=90°，∠ABC=30°，点D是边CB上任意一点，△ADE是等边三角形，且点E在∠ACB的内部，连接BE．探究线段BE与DE之间的数量关系．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．
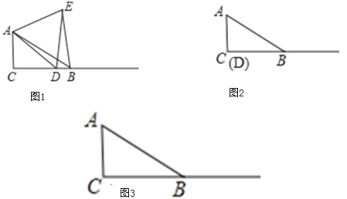
（1）当点D与点C重合时（如图2），请你补全图形．由∠BAC的度数为 ，点E落在 ______ ，容易得出BE与DE之间的数量关为 ；
（2）当点D是BC上任意一点（不与点B、C重合）时，结合图1，探究（1）中线段BE与DE之间的数量关系是否还成立？并证明你的结论．
（3）如图3，若点P为直线BC上一点，若△PAB为等腰三角形，请你求出∠APB的度数.
【答案】（1）60°；AB的中点处；BE＝DE；（2）BE＝DE依然成立，证明见解析；（3）∠APB的度数为15°或30°或75°或120°.
【解析】
（1）根据题意画出图形，由直角三角形及等边三角形的性质即可得出结论；
（2）根据题意画出图形，猜想：BE＝DE，取AB的中点F，连接EF，由∠ACB＝90°，∠ABC＝30°，可知∠1＝60°，CF＝AF＝
AB，故△ACF是等边三角形，再由△ADE是等边三角形可得出∠CAD＝∠FAE，由全等三角形的判定定理可知△ACD≌△AFE，故∠ACD＝∠AFE＝90°．由F是AB的中点，可知EF是AB的垂直平分线，进而可得出BE＝AE，结合DE＝AE可得BE＝DE；
（3）分三种情况讨论：①当AP＝AB时，②当BP＝AB时，③当AP＝BP时，根据等腰三角形的性质以及三角形内角和定理分别计算即可．
解：（1）如图2，
∵∠C＝90°，∠ABC＝30°，
∴∠BAC＝60°，
∵△ADE是等边三角形，
∴AE＝CE，
∴点E落在AB的中点处；
∴AE＝CE＝BE＝DE，
故答案为：60°；AB的中点处；BE＝DE；
（2）BE＝DE依然成立．
证明：如图3．取AB的中点F，连接EF．
∵∠ACB＝90°，∠ABC＝30°，
∴∠1＝60°，CF＝AF＝AB，
∴△ACF是等边三角形．
∴AC＝AF①，
∵△ADE是等边三角形，
∴∠2＝60°，AD＝AE②，
∴∠1＝∠2．
∴∠1＋∠BAD＝∠2＋∠BAD，即∠CAD＝∠FAE③
由①②③得△ACD≌△AFE（SAS）．
∴∠ACD＝∠AFE＝90°．
∵F是AB的中点，
∴EF是AB的垂直平分线，
∴BE＝AE，
∵△ADE是等边三角形，
∴DE＝AE，
∴BE＝DE；
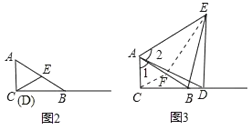
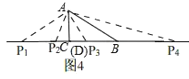
（3）如图4，
∵△PAB为等腰三角形，
∴①当AP＝AB时，即：AP1＝AB，
∴∠AP1B＝∠ABP1＝30°；
②当BP＝AB时，
Ⅰ、BP2＝AB，
∴∠AP2B＝（180°∠ABC）＝75°，
Ⅱ、BP4＝AB，
∴∠BAP4＝∠AP4B，
∵∠ABC＝30°＝∠BAP4＋∠AP4B，
∴∠AP4B＝15°；
③当AP＝BP时，即：AP3＝BP3，
∴∠BAP3＝∠ABC＝30°，
∴∠AP3B＝180°∠ABC∠BAP3＝120°，
综上所述，若△PAB为等腰三角形，∠APB的度数为15°或30°或75°或120°．
