题目内容
下列说法：①有两条直角边对应相等的两个直角三角形全等；②有斜边对应相等的两个等腰直角三角形全等；③有一条直角边和斜边上的高对应相等的两个直角三角形全等；④有一条边相等的两个等腰直角三角形全等．其中正确的有（ ）
分析：根据判定两直角三角形全等的判定方法进行判断即可．
解答：解：①有两条直角边对应相等的两个直角三角形全等，可利用SAS判定两直角三角形全等；
②有斜边对应相等的两个等腰直角三角形全等，可利用ASA判定两直角三角形全等；
③有一条直角边和斜边上的高对应相等的两个直角三角形全等，能判定两直角三角形全等；
④有一条边相等的两个等腰直角三角形全等，不能判定两直角三角形全等．
故选：C．
②有斜边对应相等的两个等腰直角三角形全等，可利用ASA判定两直角三角形全等；
③有一条直角边和斜边上的高对应相等的两个直角三角形全等，能判定两直角三角形全等；
④有一条边相等的两个等腰直角三角形全等，不能判定两直角三角形全等．
故选：C．
点评：本题考查了直角三角形全等的判定方法，直角三角形首先是三角形，所以一般三角形全等的判定方法都适合它，同时，直角三角形又是特殊的三角形，有它的特殊性，作为“HL”公理就是直角三角形独有的判定方法．所以直角三角形的判定方法最多，使用时应该抓住“直角”这个隐含的已知条件．
练习册系列答案
相关题目
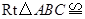
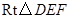，且
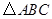的两条直角边分别是水平和竖直状态，那么
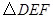的两条直角边也一定分别是水平和竖直状态
，
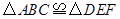，那么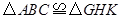
，
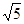，9的三角形为直角三角形； ④长方体、直六棱柱、圆锥都是多面体。