题目内容
【题目】阅读下面材料：对于平面图形A，如果存在一个圆，使图形A上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A被这个圆所覆盖．回答下列问题：
（1）边长为1cm的正方形被一个半径为r的圆所覆盖，r的最小值是______ cm；
（2）边长为1cm的等边三角形被一个半径为r的圆所覆盖，r的最小值是______ cm．
【答案】 
【解析】试题解析：(1)正方形ABCD的边长为1cm，则正方形ABCD被一个半径为r的圆所覆盖，r的最小值为其外接圆的半径，如图1，正方形ABCD的外接圆为
，
∴AC为直径，
∴r的最小值是
cm；
(2)边长为1cm的等边三角形ABC被一个半径为r的圆所覆盖,r的最小值为其外接圆的半径,如图2,等边三角形ABC的外接圆为
,
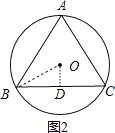
连结OB，作OD⊥BC于D，
∵点O为等边三角形ABC的外心，
∴OB平分∠ABC，
∵OD⊥BC，
在
中,∵
∴r的最小值是
cm.
故答案为： 
， 
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
