题目内容
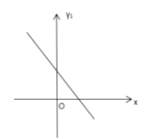
【题目】抛物线![]() 经过点A(﹣1,0)和B(2,0),直线y=
经过点A(﹣1,0)和B(2,0),直线y=![]() x+m经过点A和抛物线的另一个交点为C.
x+m经过点A和抛物线的另一个交点为C.
(1)求抛物线的解析式.
(2)动点P、Q从点A出发,分别沿线段AC和射线AO运动,运动的速度分别是每秒4个单位长度和3个单位长度.连接PQ,设运动时间为t秒,△APQ的面积为s,求s与t的函数关系式.(不写t的取值范围)
(3)在(2)的条件下,线段PQ交抛物线于点D,点E在线段AP上,且AE=AQ,连接ED,过点D作DF⊥DE交x轴于点F,当DF=![]() DE时,求点F的坐标.
DE时,求点F的坐标.
【答案】(1)![]() ;(2)S=3
;(2)S=3![]() ;(3)点F坐标为(1,0)
;(3)点F坐标为(1,0)
【解析】
(1)利用点A、B坐标,用待定系数法即求得解析式.
(2)根据题意画出PQ,易得以AQ为底来求△APQ面积较容易,故过点P作x轴的垂线PH.利用相似△对应边的比相等,用t表示PH,则写出s与t的关系式.
(3)由DE⊥DF且DF=![]() DE联想到构造相似三角形,故过点D作MN⊥x轴于点N,过点E作EM⊥MN于点M构造△NDF∽△MED,相似比为
DE联想到构造相似三角形,故过点D作MN⊥x轴于点N,过点E作EM⊥MN于点M构造△NDF∽△MED,相似比为![]() .设D(d,
.设D(d,![]() ),F(f,0),再有E的坐标可用t表示,则两相似三角形的边都能用d、t、f表示,且根据相似比为
),F(f,0),再有E的坐标可用t表示,则两相似三角形的边都能用d、t、f表示,且根据相似比为![]() 列得两个方程.又由P、Q坐标求得直线PQ的解析式(含t),点D在直线PQ上又满足解析式,列得第三个方程.解三元方程组,即求得f.
列得两个方程.又由P、Q坐标求得直线PQ的解析式(含t),点D在直线PQ上又满足解析式,列得第三个方程.解三元方程组,即求得f.
(1)∵抛物线经过点A(﹣1,0)和B(2,0),
∴ 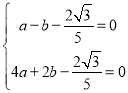 解得:
解得: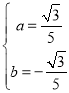
∴抛物线的解析式为 ![]() .
.
(2)设AC与y轴交点为G,过点P作PH⊥x轴于点H,
依题意得:AP=4t,AQ=3t
∵直线AC:y=![]() x+m经过点A(﹣1,0)
x+m经过点A(﹣1,0)
∴-![]() +m=0,得m=
+m=0,得m=![]()
∴直线AC解析式为:y=![]() x+
x+![]()
∴G(0,![]() ),OG=
),OG=![]()
∴AG=![]() =2
=2
∵GO∥PH
∴△
∴![]() =
=![]()
∴PH=![]() =
=![]() =2
=2![]() t
t
∴s=![]() AQPH=
AQPH=![]() t=3
t=3![]()
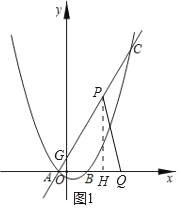
(3)过点D作MN⊥x轴于点N,过点E作EM⊥MN于点M,作ER⊥x轴于点R
∴四边形EMNR是矩形,△AGO∽△AER
∴![]() =
=![]() =
=![]()
∵AE=AQ=3t,AG=2,GO=![]() ,AO=1
,AO=1
∴MN=ER=![]() t,AR=
t,AR=![]()
∴E(﹣1+![]() ,
,![]() t)
t)
设点D(d,![]() ),F(f,0)
),F(f,0)
∴EM=d﹣(﹣1+![]() )=d+1﹣
)=d+1﹣![]() ,MD=
,MD=![]() t-
t-![]() ,DN=
,DN=![]() ,FN=d﹣f
,FN=d﹣f
∵DE⊥DF
∴∠EMD=∠EDF=∠DNF=90°
∴∠MED+∠MDE=∠MDE+∠NDF=90°
∴∠NDF=∠MED
∴△NDF∽△MED
∴![]() =
= ![]() =
= ![]() =
=![]()
∴DN=![]() EM,FN=
EM,FN=![]() MD
MD
∴![]() =
=![]() (d+1-
(d+1-![]() )①
)①
d﹣f=![]() [
[![]() -(
-(![]() )]②
)]②
∵P(﹣1+2t,2![]() t),Q(﹣1+3t,0)
t),Q(﹣1+3t,0)
∴直线PQ解析式为:y=﹣2![]() x+6
x+6![]() t﹣2
t﹣2![]()
∵点D为PQ与抛物线交点
∴﹣2![]() d+6
d+6![]() t﹣2
t﹣2![]() =
=![]() ③
③
把①③联立方程组解得: 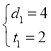 ,
,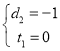 (舍去)
(舍去)
∴由②得:f=![]() +
+![]() d-
d-![]() -
-![]() t=1
t=1
∴点F坐标为(1,0)