题目内容
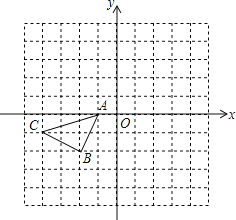
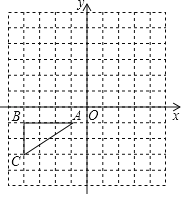
【题目】如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是( )
A.点(0，3)B.点(1，3)C.点(6，0)D.点(6，1)
【答案】B
【解析】
根据垂径定理的性质得出圆心所在位置，再根据切线的性质得出，当O'B⊥BF时F点的位置即可．
∵过格点A，B，C作一圆弧，
∴由垂径定理可得圆心为：O'(2,0)，如图所示，
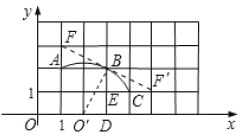
由切线性质可知当O'B⊥BF时，BF与圆相切，
当△BO'D≌△BFA时，∠O'BF=∠FBA+∠O'BA=∠O'BD+∠O'BA=90°，
此时O'B⊥BF，BF与圆相切，AF=O'D=1，AB=BD=2，
∴F坐标为（1,3），
同理可得F'（5,1），
所以满足条件的F点的坐标为：(5,1)或(1,3)，
故选B.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校开展校园“美德少年”评选活动，共有“助人为乐”，“自强自立”、“孝老爱亲”，“诚实守信”四种类别，每位同学只能参评其中一类，评选后，把最终入选的20位校园“美德少年”分类统计，制作了如下统计表，后来发现，统计表中前两行的数据都是正确的，后两行的数据中有一个是错误的．
类别 | 频数 | 频率 |
助人为乐美德少年 | a | 0.20 |
自强自立美德少年 | 3 | b |
孝老爱亲美德少年 | 7 | 0.35 |
诚实守信美德少年 | 6 | 0.32 |
根据以上信息，解答下列问题：
（1）统计表中的a＝ ，b ；
（2）统计表后两行错误的数据是 ，该数据的正确值是 ；
（3）校园小记者决定从A，B，C三位“自强自立美德少年”中随机采访两位，用画树状图或列表的方法，求A，B都被采访到的概率．
