题目内容
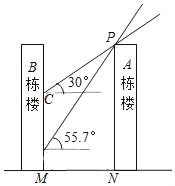
【题目】如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
【答案】(1)50;(2)21层
【解析】
(1)根据三角函数的性质,设PE=x,在直角三角形PCE中表示出CE,利用CE=DF=MN,在直角三角形PDF中用三角函数即可求出结论,(2)根据上一问求出PE的长,进而求出CM的长,利用每层楼高3米即可解题.
解:(1)过点C作CE⊥AN与E, 过点D作DF⊥AN与F,
设AE=x,
∵∠C=30°,
∴CE=1.72x,EF=44.5,
在△PDF中,DF=![]() =50,
=50,
(2)由(1)知,CE=50,PE=CEtan30°=50![]() 0.58=29,
0.58=29,
∴CM=61,
∵每层高均为3m,
∴点C位于第21层.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目