题目内容
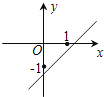
【题目】某市规定了每月用水18立方米以内（含18立方米）和用水18立方米以上两种不同的收费标准，该市的用户每月应交水费y（元）是用水量x（立方米）的函数，其图象如图所示．
（1）若某月用水量为18立方米，则应交水费多少元？
（2）求当x＞18时，y关于x的函数表达式，若小敏家某月交水费81元，则这个月用水量为多少立方米？
【答案】（1）45；（2）30．
【解析】
试题分析：（1）根据函数图象上点的纵坐标，可得答案；
（2）根据待定系数法，可得函数解析式，根据自变量与函数值得对应关系，可得答案．
试题解析：（1）由纵坐标看出，某月用水量为18立方米，则应交水费45元；
（2）由81元＞45元，得用水量超过18立方米，设函数解析式为y=kx+b （x≥18），∵直线经过点（18，45）（28，75），∴
，解得：
，∴函数的解析式为y=3x﹣9 （x≥18），当y=81时，3x﹣9=81，解得x=30．
答：这个月用水量为30立方米．
练习册系列答案
阅读快车系列答案
相关题目
【题目】(2016·天津)公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台，租车费用为400元，每辆乙种货车一次最多运送机器30台，租车费用为280元．
(1)设租用甲种货车x辆(x为非负整数)，试填写表格：
表一：
租用甲种货车的数量 / 辆 | 3 | 7 | x |
租用的甲种货车最多运送机器的数量 / 台 | 135 | ||
租用的乙种货车最多运送机器的数量 / 台 | 150 |
表二：
租用甲种货车的数量 / 辆 | 3 | 7 | x |
租用甲种货车的费用/ 元 | 2800 | ||
租用乙种货车的费用 / 元 | 280 |
(2)若租用甲种货车x辆时，设两种货车的总费用为y元，试确定能完成此项运送任务的最节省费用的租车方案．
