题目内容
【题目】直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】如图,分别过点A、B、D作AF⊥l3 , BE⊥l3 , DG⊥l3 ,
∵△ABC是等腰直角三角形,∴AC=BC.
∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,∴∠EBC=∠ACF,∠BCE=∠CAF.
在△BCE与△ACF中,∵∠EBC=∠ACF,BC=AC,∠BCE=∠CAF,∴△BCE≌△ACF(ASA).
∴CF=BE=3,CE=AF=4.
在Rt△ACF中,∵AF=4,CF=3,∴![]() .
.
∵AF⊥l3 , DG⊥l3 , ∴△CDG∽△CAF. ∴![]() ,即
,即![]() ,解得
,解得![]() .
.
在Rt△BCD中,∵![]() ,BC=5,∴
,BC=5,∴![]() .
.
故选A.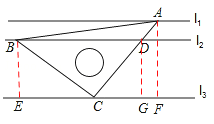
【考点精析】本题主要考查了等腰直角三角形和平行线之间的距离的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离才能正确解答此题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目